Katalytische Verzweigungsstrukturen

Bearbeiter: K. Fleischmann  

Kooperation: D. A. Dawson (Fields Institute, Toronto), A. M. Etheridge (Queen Mary and Westfield College, London), M. A. Kouritzin (University of Alberta, Edmonton), A. Klenke (Friedrich-Alexander-Universität Erlangen-Nürnberg), G. Leduc (Université du Quebec, Montréal), C. Mueller (University of Rochester), V. A. Vatutin (Steklov Mathematical Institute, Moskau)

Beschreibung der Forschungsarbeit: Eine ausführliche Beschreibung der Motivation für dieses Forschungsgebiet wurde im Jahresforschungsbericht 1995, S. 133, gegeben. Im Mittelpunkt der Tätigkeit in diesem Berichtsjahr stand die vertiefte Untersuchung der stetigen Super-Brownschen Bewegung $\,X^\varrho \,$in einem Super-Brownschen Medium $\,\varrho \,$ ([1]). Dies beschreibt eine Population von Teilchen, die sich im ${\sf R}^d$ chaotisch bewegen und kritisch binär verzweigen. Die Verzweigung ist nur in Gegenwart von Katalysatoren möglich, die sich selbst auch chaotisch bewegen und kritisch binär verzweigen. Die Abbildung zeigt eine zweidimensionale Simulation.

In diesem Jahr stand die Untersuchung der lokalen Struktur dieser katalytischen Super-Brownschen Bewegung $\,X^\varrho \,$ im Mittelpunkt der Untersuchungen. Es wurde nachgewiesen ([5]), daß in den Dimensionen 2 und 3 außerhalb des Katalysators (der sich in Lebesgue Nullmengen befindet) die Populationen glatte Dichten besitzen, welche die Wärmeleitungsgleichung lösen. In der kritischen Dimension 2 folgt dann mit Selbstähnlichkeitsargumenten, daß im lokalen Langzeitverhalten Konvergenz gegen eine gleichmäßig verteilte Grenzpopulation $\,X_\infty ^\varrho \,$ mit zufälliger Intensität unendlicher Erwartung stattfindet, im Unterschied zur Dimension 3, [2]. (Persistenz war bereits im Vorjahr gezeigt worden, [4].)

Eine weitere Aktivität bestand darin, das Langzeitverhalten markierter Teilchensysteme zu untersuchen ([6]; DFG-Unterstützung: 436 RUS 17/112/96). Dies ist eng verbunden mit dem Studium von L¹-Normen von (nicht-negativen) Lösungen von Reaktions-Diffusions-Systemen. Eine Dichotomie bezüglich lokalem Sterben und Überleben wurde unter ziemlich allgemeinen, natürlichen Bedingungen nachgewiesen.

Schließlich wurde eine Arbeit zur allgemeinen Strukturtheorie von Superprozessen vollendet ([3]).

Projektliteratur:

1.   D. A. DAWSON, K. FLEISCHMANN, A continuous super-Brownian motion in a super-Brownian medium, J. Theoret. Probab., 10(1) (1997), pp. 213-276.
2.   D. A. DAWSON, K. FLEISCHMANN, Longtime behavior of a branching process controlled by branching catalysts, Stochastic Process. Appl., 71(2) (1997), pp. 241-257.
3.   D. A. DAWSON, K. FLEISCHMANN, G. LEDUC. Continuous dependence of a class of superprocesses on branching parameters, and applications, WIAS-Preprint No. 317 (1997), eingereicht bei: Ann. Probab.
4.   A. M. ETHERIDGE, K. FLEISCHMANN. Persistence of a two-dimensional super-Brownian motion in a catalytic medium, WIAS-Preprint No. 277 (1996), erscheint in: Probab. Theory Related Fields, 110(1) (1998).
5.   K. FLEISCHMANN, A. KLENKE. Smooth density field of catalytic super-Brownian motion, WIAS-Preprint No. 331 (1997), eingereicht bei: Ann. Appl. Probab.
6.   K. FLEISCHMANN, V. A. VATUTIN, Long-term behavior of a critical multitype spatially homogeneous branching particle process and a related reaction-diffusion system, WIAS-Preprint No. 350 (1997).

The first row shows a discrete version of $\varrho$ (critical binary branching simple random walk) on a $250\times 250$ grid with periodic boundaries, originally started from a ``uniformly'' distributed field. The number of particles per site is indicated by different grey scales. The ``movie'' clearly exhibits the well-known tendency of clustering in d=2.

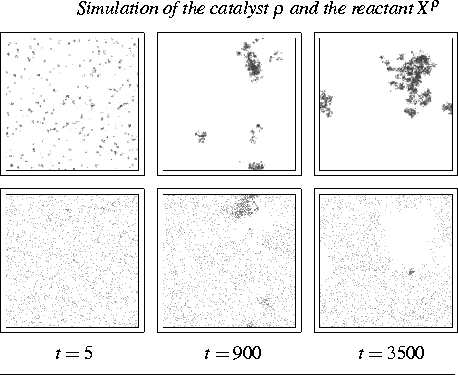
The second sequence of pictures shows a simulation of the analogous discrete version of $X^\varrho ,$ for the same realization of the branching rate $\varrho .$ The figure illustrates that the reactant $X^\varrho$is uniformly spread out outside the catalytic clusters, except a few ``hot spots'' related to the catalyst, and that within the catalytic clumps mainly killing of the reactant happens.