Bearbeiter: J. Elschner , J. Niebsch , S. Prößdorf , G. Schmidt
Kooperation: V. G. Maz'ya, T. Ivanov (Universität Linköping), G. Monegato (Technische Universität Turin), O. Hansen (Universität Mainz)
Beschreibung der Forschungsarbeit:
Die Bestimmung der für die Bruchmechanik wichtigen K-Faktoren erfordert die Lösung von Randwertproblemen der linearen Elastizitätstheorie. Dabei erweist sich der Einsatz von Integralgleichungs- und Randelementmethoden oft als effektiver als die Verwendung von Finite-Elemente-Methoden. Zum Beispiel führt die Behandlung der ersten Randwertaufgabe der Elastizitätstheorie auf die Integralgleichung von Lauricella-Sherman:
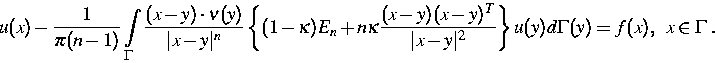 |
(1) |
In [1] wurden mit Hilfe von Mellin-Techniken neue Resultate zur Existenz, Eindeutigkeit und Regularität in Lp-Räumen und Sobolewräumen mit Gewicht für die Integralgleichung (1) auf dem Rand eines ebenen Gebietes mit Ecken erzielt. Auf der Grundlage dieser Lösbarkeitstheorie gelang es erstmalig, die Stabilittät von Kollokationsverfahren mit stückweise polynomialen Ansatzfunktionen (Splines) im Fall polygonaler Gebiete zu begründen. Des weiteren wurde gezeigt, daß diese Verfahren bei Verwendung graduierter Gitter eine optimale Konvergenzordnung aufweisen.
Gegenwärtig beschäftigen wir uns mit dem (wesentlich schwierigeren) Problem der analytischen und numerischen Behandlung von Randintegralgleichungen der Elastizitätstheorie über 3D-Gebieten mit nichtglattem Rand (z. B. Polyedergebiete). Erste Untersuchungen zu einer Lösbarkeits- und Regularitätstheorie in geeigneten gewichteten Sobolewräumen für die Integralgleichung (1) auf einem Polyederrand wurden begonnen.
Verschiedene Kontaktprobleme der ebenen Elastizitätstheorie führen auf die Integralgleichung 1. Art
mit gegebenen Konstanten ![]() und
und ![]() ,
, ![]() , und einer
bekannten Funktion G. Gesucht ist eine symmetrische Lösung F von
(2), die der Bedingung
, und einer
bekannten Funktion G. Gesucht ist eine symmetrische Lösung F von
(2), die der Bedingung
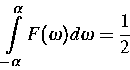 |
(2) |
Durch Anwendung des Differentialoperators ![]() und der anschließenden Variablentransformation
und der anschließenden Variablentransformation ![]() wurde in [5] das Problem (2),
(3) auf die Gleichung
wurde in [5] das Problem (2),
(3) auf die Gleichung
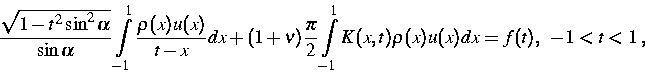 |
(3) |
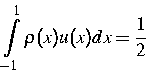 |
(4) |
Iterative Integralgleichungsmethoden sind ein interessantes alternatives Lösungsverfahren für nichtlineare Randwertaufgaben, insbesondere wenn diese auch Integraloperatoren mit singulären Kernfunktionen enthalten. Durch Anwendung einer von V. Maz'ya vorgeschlagenen Approximationsmethode mittels glatter, schnell abfallender Funktionen und daraus abgeleiteter effektiver Kubaturformeln für verschiedene singuläre Integrale und Potentiale (vgl. [4]) wurden von Maz'ya/Karlin [3] unter anderem Zeitschrittverfahren zur Lösung von Evolutionsproblemen entwickelt, die bei numerischen Tests zur Lösung von Anfangswertproblemen verschiedener Klassen von Gleichungen sehr genaue Resultate liefern. Die theoretische Untersuchung des Konvergenzverhaltens dieser Verfahren wird durch das Auftreten von sogenannten Sättigungsfehlern bei der Approximation erschwert. 1997 wurden erste Arbeiten zur numerischen Analysis solcher Verfahren für einen wichtigen Spezialfall durchgeführt. Insbesondere wurden Fehlerabschätzungen theoretisch begründet sowie die optimale Wahl von Parametern untersucht. Es ist vorgesehen, diese Ergebnisse u. a. auf Gleichungen aus der Dislokations- und Plastizitätstheorie zu verallgemeinern. Hierbei ist ein in [2] entwickelter Zugang für die Kubatur von Integraloperatoren in beschränkten Gebieten anzuwenden, der auf der Quasiinterpolation der Dichte auf speziellen, sich zum Rand hin häufenden Gitterpunkten basiert.
Projektliteratur: