




Next: Multiskalen-Methoden
Up: Projektbeschreibungen
Previous: Behandlung von Problemen der Bruchmechanik und
Bearbeiter: G. Bruckner
,S. Prößdorf
Kooperation: W. Dahmen,
K. Urban (Rheinisch-Westfälische Technische
Hochschule Aachen),
W. Mc Lean,
I. H. Sloan (University of New South Wales, Sydney)
Kooperation: J. Cheng (Fudan University, Shanghai),
S. V. Pereverzev (Ukrainische Akademie der
Wissenschaften, Kiew),
M. Yamamoto (University of Tokyo)
Beschreibung der Forschungsarbeit:
1. Die behandelte Aufgabe aus der Seismik betrifft die
schwingende Saite im eindimensionalen, bzw. die
schwingende Membran im zweidimensionalen Fall, die am Rande eingespannt ist
und durch Auslenkung in endlich vielen Punkten in Erregung versetzt wird.
Durch geeignete Messungen im Inneren oder auf dem Rande sollen die
Erregungsherde identifiziert werden.
Mathematisch handelt es sich im eindimensionalen Falle beim direkten Problem
um das
folgende Rand-Anfangswertproblem für die Wellengleichung:
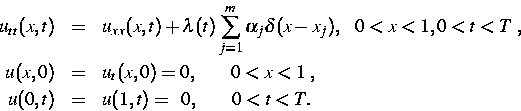
Hier sind die reellen Zahlen ![$\alpha_j, x_j\in (0,1), 1\le j\le m,\;
\lambda \in C^1[0,1],
\lambda (0)\neq 0,$](../../1997/html/images/img213.gif) gegeben, und
gegeben, und 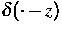 ist die Diracsche
Distribution mit
ist die Diracsche
Distribution mit 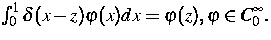
Das inverse Problem besteht in der Bestimmung der Parametermenge
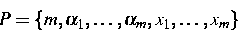
aus der Beobachtung beispielsweise von u(y0,t),0<t<T, für fixiertes
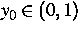 .
.
Im eindimensionalen Fall gelang es, das
Problem in ein nichtlineares gutgestelltes Problem und eine lineare
Operatorgleichung, eine Integralgleichung erster Art,
zu zerlegen und für letztere Regularisierungsverfahren anzugeben
(vgl. [1]),
die auf einer Datenglättung beruhen.
In [2] wurde außer gestörten Meßdaten zusätzlich ein gestörter
Operator betrachtet. Das bedeutet speziell für das genannte
Anwendungsproblem,
daß die Funktion 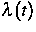 nicht exakt gegeben ist. Für eine
Operatorgleichung
nicht exakt gegeben ist. Für eine
Operatorgleichung
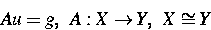
mit gestörtem Operator und gestörter rechter Seite wurde
das folgende Konzept entwickelt.
Wir gehen davon aus, daß eingehende Fehler unterschiedlicher Natur
sein können. So kann eine Funktion beispielsweise an diskreten Stellen
ungenau gemessen, oder sie kann durch weißes Rauschen verfälscht sein.
Man hat daher den Fehler nicht nur nach seiner Größe, sondern auch nach
seiner Qualität zu unterscheiden. Damit ist klar, daß Fehler, die in den
Operator und solche, die in die Daten (=rechte Seite) eingehen,
sich im allgemeinen
qualitativ und quantitativ unterscheiden werden.
Um die Qualität der Fehler
beschreiben zu können, nehmen wir an, daß Y in eine Skala von
Banachräumen eingebettet ist,

Die Güte des gestörten Operators 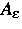 charakterisieren wir dann
durch die Nummer
charakterisieren wir dann
durch die Nummer 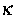 , für die die Operatornorm
, für die die Operatornorm
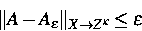
ist, und die Glattheit der Daten 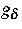 durch die
Nummer
durch die
Nummer 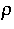 , für die
, für die
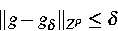
gilt.
Es wurden, ausgehend von einem numerischen Verfahren bei exaktem
Operator und exakter rechter Seite, Fehlerabschätzungen bei
gestörtem Operator und gestörter rechter Seite unter Berücksichtigung
der unterschiedlichen Qualität dieser Störungen abgeleitet (vgl. [2]).
Der Grundgedanke ist, das Gesamtproblem in einen operatorspezifischen Anteil
und einen datenspezifischen Anteil zu zerlegen.
2. Verschiedene Probleme der lokalen Tomographie, der Armierung
von Stahlbeton sowie der Geophysik führen auf eine Integralgleichung
1. Art der Gestalt
| 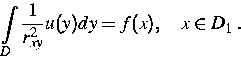 |
(1) |
Hierbei bezeichnet rxy=|x-y| den Euklidischen Abstand der Punkte
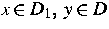 , und
, und 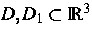 sind einfach
zusammenhängende Gebiete mit leerem Durchschnitt. Weil die Kernfunktion
r-2xy in beiden Variablen analytisch ist, ist das Problem
(1) hochgradig schlecht gestellt. Da die Singulärwerte des
Integraloperators (1) sehr schnell gegen Null abklingen, ist
es äußerst schwierig, eine gute Approximationslösung für (1)
zu finden. Für die numerische Analysis der Gleichung (1) sind
lokale (besonders punktweise) Stabilitätsabschätzungen der (i. a. nur
lokal glatten) Lösung von besonderer Bedeutung. Dazu gibt es in der
Literatur bisher so gut wie keine Ergebnisse. In [3] wurden
lokale punktweise Stabilitätsabschätzungen vom logarithmischen Typ bei
Benutzung der Energienorm von f gefunden unter der Annahme, daß die
Lösung
sind einfach
zusammenhängende Gebiete mit leerem Durchschnitt. Weil die Kernfunktion
r-2xy in beiden Variablen analytisch ist, ist das Problem
(1) hochgradig schlecht gestellt. Da die Singulärwerte des
Integraloperators (1) sehr schnell gegen Null abklingen, ist
es äußerst schwierig, eine gute Approximationslösung für (1)
zu finden. Für die numerische Analysis der Gleichung (1) sind
lokale (besonders punktweise) Stabilitätsabschätzungen der (i. a. nur
lokal glatten) Lösung von besonderer Bedeutung. Dazu gibt es in der
Literatur bisher so gut wie keine Ergebnisse. In [3] wurden
lokale punktweise Stabilitätsabschätzungen vom logarithmischen Typ bei
Benutzung der Energienorm von f gefunden unter der Annahme, daß die
Lösung 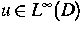 eine
gewisse minimale lokale Glattheit besitzt.
eine
gewisse minimale lokale Glattheit besitzt.
3. In [4] wurde eine Methode der stückweise konstanten
Approximation der Lösung der (schlecht gestellten) Volterraschen
Integralgleichung 3. Art
![\begin{displaymath}
p(t)z(t)+
\int\limits^t_0 \frac{h(t,\tau)}{(t-\tau)^{1-\alpha}}
z(\tau)d\tau = f(t),\;t\in [0,1]\;,\; 0<\alpha<1\;,\end{displaymath}](../../1997/html/images/img231.gif)
entwickelt. Hierbei ist p eine Funktion, die auf einer Punktmenge
des Intervalls ![$[t_1 ,t_2]\subset [0,1]$](../../1997/html/images/img232.gif) verschwindet und außerdem die
Abschätzung
verschwindet und außerdem die
Abschätzung 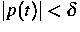 für alle
für alle ![$t\in [t_1 ,t_2]$](../../1997/html/images/img234.gif) erfüllt, wobei
erfüllt, wobei
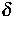 eine hinreichend kleine positive Zahl ist. Die vorgeschlagene
Methode liefert eine Genauigkeit der Ordnung
eine hinreichend kleine positive Zahl ist. Die vorgeschlagene
Methode liefert eine Genauigkeit der Ordnung
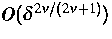 bezüglich der L2-Norm, wobei
bezüglich der L2-Norm, wobei 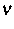 der
Parameter der quellenweisen Darstellung der exakten Lösung auf dem
Intervall [t1 ,t2] ist. Der entwickelte Algorithmus benutzt nicht
mehr als
der
Parameter der quellenweisen Darstellung der exakten Lösung auf dem
Intervall [t1 ,t2] ist. Der entwickelte Algorithmus benutzt nicht
mehr als 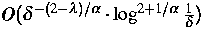 Werte der Galerkinschen Funktionale, wobei
Werte der Galerkinschen Funktionale, wobei
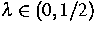 im Prozeß der Bestimmung des
Regularisierungsparameters (nach dem Morozovschen Diskrepanzprinzip)
gewählt wird.
im Prozeß der Bestimmung des
Regularisierungsparameters (nach dem Morozovschen Diskrepanzprinzip)
gewählt wird.
Projektliteratur:
- G. BRUCKNER, On the regularization of an inverse
vibration problem, GAMM-Tagung 1997, eingereicht.
- G. BRUCKNER, On an operator equation with noise
in the operator and the right-hand side with application to an
inverse vibration problem, in Vorbereitung.
- J. CHENG, S. PRÖSSDORF, M. YAMAMOTO, Local
estimation for an integral equation of first kind with analytic
kernel, in Vorbereitung.
- S. V. PEREVERZEV, S. PRÖSSDORF, A
discretization of Volterra integral equations of third kind
with weakly singular kernels, WIAS-Preprint No. 374,
1997, erscheint in: J. of Inverse and Ill-Posed Problems.





Next: Multiskalen-Methoden
Up: Projektbeschreibungen
Previous: Behandlung von Problemen der Bruchmechanik und
LaTeX typesetting by I. Bremer
1/18/1999
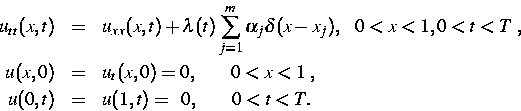
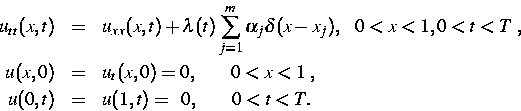
![]()
![]() nicht exakt gegeben ist. Für eine
Operatorgleichung
nicht exakt gegeben ist. Für eine
Operatorgleichung
![]()
![]()
![]()
![]()
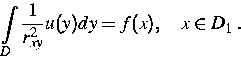
![\begin{displaymath}
p(t)z(t)+
\int\limits^t_0 \frac{h(t,\tau)}{(t-\tau)^{1-\alpha}}
z(\tau)d\tau = f(t),\;t\in [0,1]\;,\; 0<\alpha<1\;,\end{displaymath}](../../1997/html/images/img231.gif)