




Next: Behandlung von Problemen der Bruchmechanik und
Up: Projektbeschreibungen
Previous: Direkte und inverse Probleme für diffraktive
Subsections
Bearbeiter: R. Henrion
,
A. Möller
Kooperation: P. Li (TU Berlin), W. Römisch (HU Berlin),
G. Wozny (TU Berlin), J. Mayer (ETH Zürich), M. Steinbach
(ZIB Berlin), P. Szantai (TU Budapest)
Förderung: DFG-Schwerpunktprogramm ,,Echtzeitoptimierung großer Systeme``
Beschreibung der Forschungsarbeit:
Gegenstand des Projekts (Beginn: 01.10.1997) ist die Optimierung integrierter
Kolonnensysteme unter stochastischen Echtzeitbedingungen. Das Ziel besteht
in der Ermittlung einer online zu bestimmenden robusten, optimalen
Führungsstrategie.
Aus wirtschaftlichen und ökologischen Gründen ist die Senkung des
Energieverbrauchs von thermischen Destillationsprozessen in der chemischen
Industrie erforderlich. Durch Verwendung energetisch gekoppelter
Destillationskolonnen läßt sich der Energiebedarf bereits wesentlich
reduzieren, doch ist dies mit einer schwierigeren Steuerung, Regelung und
Optimierung der Prozesse verbunden. Der konventionelle Betrieb integrierter
Kolonnensysteme basiert auf der vorherigen Auslegung für einen konstanten
Betriebspunkt. In der Realität ändern sich jedoch die Randbedingungen, so
daß die Prozesse am vorgegebenen Betriebspunkt energetisch nicht optimal
betrieben werden können. Daraus ergibt sich die Notwendigkeit der
Echtzeit-Optimierung unter Berücksichtigung der sich ändernden
Randbedingungen. Der sowohl nach Menge als auch Zusammensetzung stochastisch
variierende Feed des Prozesses besitzt wesentlichen Einfluß auf die
Einhaltung der geforderten Produktspezifikationen.
In dieser Arbeit wird der bisher in der Literatur nicht betrachtete Fall
einer Feedänderung von 2t/h bis 6t/h und einer Änderung der
Feedkonzentration von ca. 3% Methanol (Strahlerwässer) auf
35-40% Methanol (Produkte aus Veresterungsprozessen) untersucht.
Es muß ein Vollastbetrieb mit hohen Lasten (6t/h) und unterschiedlichen
Eingangskonzentrationen ebenso wie z. B. am Wochenende Teillast (2t/h) zum
Warmhalten der Kolonnen realisiert werden können. Hier liegt die besondere
wissenschaftliche Herausforderung bezüglich der Echtzeit-Optimierung
des Energieverbrauchs bei gleichzeitiger Einhaltung aller
Produktanforderungen und der gegebenen Anlagenbegrenzungen.
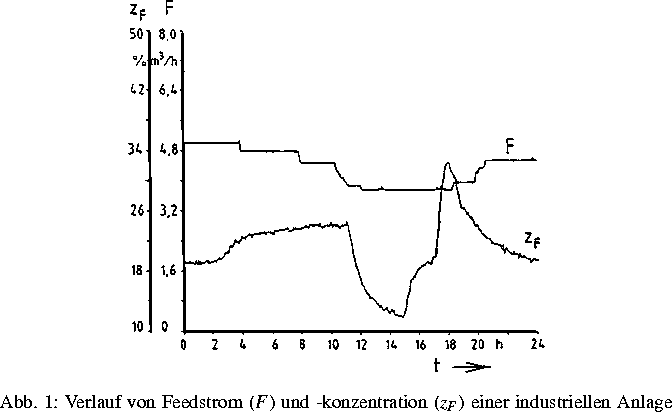
In Abbildung 1 ist ein im Rahmen der Vorarbeiten
aufgenommener Konzentrations- und Feedmengenverlauf einer typischen
Produktionsanlage ohne energetische Kopplung für den Zeitraum von 24
Stunden exemplarisch dargestellt.
Das dem zu untersuchenden Prozeß zugrundeliegende dynamische Modell wird
durch ein semi-explizites differentiell-algebraisches Gleichungssystem
beschrieben. Die Besonderheit des hier gewählten Zugangs besteht darin,
daß die herkömmlich deterministisch formulierten Nebenbedingungen
für die Produktspezifikationen und die Realisierung einer Mindestfeedmenge
im Tank als Wahrscheinlichkeitsrestriktionen
aufgefaßt werden, um deren stochastische Abhängigkeit vom Feed
mit dem Ziel der Ermittlung einer robusten Strategie zu berücksichtigen.
Die Produktspezifikationen lassen sich in der Form
![\begin{displaymath}
h_1(x_{u,\xi}(t))\geq\alpha_1,\quad \forall t\in [t_0,t_1]\end{displaymath}](../../1997/html/images/img191.gif)
schreiben, wobei 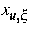 die von der Steuerung u und der
zufälligen Zusammensetzung
die von der Steuerung u und der
zufälligen Zusammensetzung 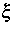 des Feeds abhängige Konzentration
der interessierenden Komponente und h1 eine gewisse Funktion
dieser Konzentration ist.
des Feeds abhängige Konzentration
der interessierenden Komponente und h1 eine gewisse Funktion
dieser Konzentration ist.
Die Realisierung einer Mindestmenge im Tank,
wodurch insbesondere am Wochenende das Warmhalten der Kolonnen abzusichern
ist, kann als
![\begin{displaymath}
h_2(u(t),\eta (t))\geq\alpha_2,\quad\forall t\in [t_0,t_1]\end{displaymath}](../../1997/html/images/img194.gif)
dargestellt werden. Hier ist h2 eine Funktion der Steuerung sowie der
zufälligen Feedmenge 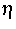 , die dem Tank zufließt.
Eine Möglichkeit, die beiden Nebenbedingungen als
Wahrscheinlichkeitsrestriktionen
zu formulieren, ergibt sich aus
, die dem Tank zufließt.
Eine Möglichkeit, die beiden Nebenbedingungen als
Wahrscheinlichkeitsrestriktionen
zu formulieren, ergibt sich aus
![\begin{eqnarray*}
P^\xi (h_1(x_{u,\xi}(t))\geq\alpha_1\,\,\forall t\in [t_0,t_1]...
...2(u(t),\eta (t))\geq\alpha_2\,\,\forall t\in [t_0,t_1])&\geq&p_2.\end{eqnarray*}](../../1997/html/images/img195.gif)
Eine andere Variante besteht in der Aufstellung punktweiser
Wahrscheinlichkeitsrestriktionen der Gestalt
![\begin{eqnarray*}
P^\xi (h_1(x_{u,\xi}(t))\geq\alpha_1)&\geq&p_1,\quad\forall t\...
...u(t),\eta (t))\geq\alpha_2)&\geq&p_2,\quad\forall t\in [t_0,t_1].\end{eqnarray*}](../../1997/html/images/img196.gif)
Bei Verwendung dieser zweiten Variante läßt sich das zu analysierende
stochastische Optimierungsproblem zusammenfassend
folgendermaßen formulieren:
![\begin{eqnarray*}
J(u)\Longrightarrow {\rm Min}&&{\rm bei}\ x_{u,\xi}'(t)&=&f(x...
...t),\eta (t)))\geq\alpha_2&\geq&p_2\;,\quad\forall t\in [t_0,t_1].\end{eqnarray*}](../../1997/html/images/img197.gif)
Hierbei ist J ein Energiefunktional, und g beschreibt den
algebraischen Zusammenhang der Zustandsgrößen.
Für die Behandlung der Wahrscheinlichkeitsrestriktionen innerhalb des
Optimierungsproblems ist die nähere Analyse der stochastischen Prozesse
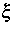 und
und 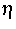 erforderlich. Hierbei soll die Gültigkeit
geeigneter Annahmen geprüft werden, die diese Nebenbedingungen einer
numerischen Realisierung zugänglich machen.
Zunächst soll vorausgesetzt werden, daß es sich bei
erforderlich. Hierbei soll die Gültigkeit
geeigneter Annahmen geprüft werden, die diese Nebenbedingungen einer
numerischen Realisierung zugänglich machen.
Zunächst soll vorausgesetzt werden, daß es sich bei 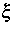 und
und
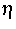 um Gaußsche Prozesse handelt. Später werden auch
Markov-Prozeß-Eigenschaften untersucht. Zur Einbindung in die
Realisierung der Lösung des Optimierungsproblems mittels SQP-Verfahren sind
sowohl analytisch gewonnene Informationen [5]
über die Werte und die Ableitung der die Wahrscheinlichkeitsrestriktion
beschreibenden
Abbildung nach der Steuervariablen u als auch die Berechnung von
Schranken mittels Monte-Carlo-Methoden von Bedeutung
[4]. Zur Charakterisierung des
stochastischen Modells und eventuell auch zu seiner Optimierung ist die
Simulation des stochastischen Feed-Prozesses notwendig [1].
Das hochdimensionale Steuerungsproblem soll durch Anwendung direkter
Kollokations- oder
Schießverfahren zur Diskretisierung in Verbindung mit
strukturorientierten SQP-Verfahren gelöst werden. Hierzu ist durch
eingehendere Modellanalyse zu prüfen, welche der in der Literatur
beschriebenen modernen Methoden sowie welche verfügbare effiziente Software
[2,3]
im vorliegenden Fall am besten dem Echtzeitcharakter der
Problematik entsprechen.
um Gaußsche Prozesse handelt. Später werden auch
Markov-Prozeß-Eigenschaften untersucht. Zur Einbindung in die
Realisierung der Lösung des Optimierungsproblems mittels SQP-Verfahren sind
sowohl analytisch gewonnene Informationen [5]
über die Werte und die Ableitung der die Wahrscheinlichkeitsrestriktion
beschreibenden
Abbildung nach der Steuervariablen u als auch die Berechnung von
Schranken mittels Monte-Carlo-Methoden von Bedeutung
[4]. Zur Charakterisierung des
stochastischen Modells und eventuell auch zu seiner Optimierung ist die
Simulation des stochastischen Feed-Prozesses notwendig [1].
Das hochdimensionale Steuerungsproblem soll durch Anwendung direkter
Kollokations- oder
Schießverfahren zur Diskretisierung in Verbindung mit
strukturorientierten SQP-Verfahren gelöst werden. Hierzu ist durch
eingehendere Modellanalyse zu prüfen, welche der in der Literatur
beschriebenen modernen Methoden sowie welche verfügbare effiziente Software
[2,3]
im vorliegenden Fall am besten dem Echtzeitcharakter der
Problematik entsprechen.
Projektliteratur:
- U. M. DIWEKAR, J. R. KALAGNANAM,
Efficient sampling technique for optimization under uncertainty,
AIChE J., 43 (1997), pp. 440-447.
- P. E. GILL, W. MURRAY, M. A. SAUNDERS,
Large scale SQP methods and their application in trajectory
optimization,
in: Computational Optimal Control (R. Bulirsch, D. Kraft, eds.),
Birkhäuser, Basel, 1994, pp. 29-42.
- M. HEINKENSCHLOSS,
Projected Sequential Quadratic Programming Methods,
SIAM J. Optim., 6 (1996), pp. 373-417.
- A. PRéKOPA,
Sharp bounds on probabilities using linear programming,
Oper. Res., 38 (1990), pp. 227-239.
- S. URYASEV,
Derivatives of probability functions and some applications,
Ann. Oper. Res., 56 (1995), pp. 287-311.





Next: Behandlung von Problemen der Bruchmechanik und
Up: Projektbeschreibungen
Previous: Direkte und inverse Probleme für diffraktive
LaTeX typesetting by I. Bremer
1/18/1999

![]()
![]()
![\begin{eqnarray*}
P^\xi (h_1(x_{u,\xi}(t))\geq\alpha_1\,\,\forall t\in [t_0,t_1]...
...2(u(t),\eta (t))\geq\alpha_2\,\,\forall t\in [t_0,t_1])&\geq&p_2.\end{eqnarray*}](../../1997/html/images/img195.gif)
![\begin{eqnarray*}
P^\xi (h_1(x_{u,\xi}(t))\geq\alpha_1)&\geq&p_1,\quad\forall t\...
...u(t),\eta (t))\geq\alpha_2)&\geq&p_2,\quad\forall t\in [t_0,t_1].\end{eqnarray*}](../../1997/html/images/img196.gif)
![\begin{eqnarray*}
J(u)\Longrightarrow {\rm Min}&&{\rm bei}\ x_{u,\xi}'(t)&=&f(x...
...t),\eta (t)))\geq\alpha_2&\geq&p_2\;,\quad\forall t\in [t_0,t_1].\end{eqnarray*}](../../1997/html/images/img197.gif)