Direkte und inverse Probleme für diffraktive Strukturen in der Optik

Bearbeiter: J.  Elschner, R.  Hinder, G.  Schmidt,  

Kooperation: B. Kleemann, H.-J. Rostalski (Berliner Institut für Optik GmbH (BIFO))

Förderung: BMBF

Beschreibung der Forschungsarbeit:

Die Entwicklung verschiedener hochpräziser Mikro-Techniken erlaubt die Herstellung komplexer Oberflächenprofile, die als hocheffektive optische Gitter und andere diffraktive Strukturen eingesetzt werden können und deren Nutzung in verschiedenen Bereichen der Verfahrens-, Umwelt- und Medizintechnik enorme Potentiale bietet. Bei der Modellierung und Berechnung solcher Strukturen stoßen die bisher in der optischen Beugungstheorie benutzten Ansätze der geometrischen Optik an ihre Grenzen. Deshalb entsteht bei der praktischen Anwendung moderner diffraktiver Technologien ein wachsendes Bedürfnis nach einer exakteren Modellierung, die auf den elektro-magnetischen Feldgleichungen basiert, und nach der Entwicklung effektiver analytischer und numerischer Lösungsmethoden, um das Verhalten vorgegebener Strukturen zu beschreiben und um andererseits Strukturen zu bestimmen, die vorgegebene optische Eigenschaften besitzen.

Die Arbeiten zu dieser Thematik werden im Rahmen des vom BMBF geförderten Projekts ,,Analytische und numerische Behandlung direkter und inverser Probleme für diffraktive Strukturen - Optimierung binärer optischer Gitter`` und auf der Grundlage einer Forschungsvereinbarung mit dem BIFO durchgeführt. Der Schwerpunkt hierbei liegt auf binären und Multilevel-Gittern, deren Herstellung weitgehend beherrscht wird und die ein breites Anwendungsspektrum besitzen.

1997 wurden zu dieser Thematik folgende Arbeiten durchgeführt:

1. Abschluß der analytischen Untersuchungen des klassischen Diffraktionsproblems für Gitter mit stückweise glatten Profilen:

In [2] wurden ausgehend von einer auf Bao/Dobson/Friedman (vgl. [1]) zurückgehenden Variationsformulierung Existenz- und Eindeutigkeitsaussagen sowie Stabilitätskriterien für die numerische Lösung des direkten Problems erzielt, die bekannte Aussagen aus der Literatur wesentlich verallgemeinern. Des weiteren wurden exakte analytische Gradientenformeln zur Lösung des optimalen Design-Problems bei beschichteten binären Gittern auf Multilayer-Systemen angegeben und begründet (vgl. [3]).

2. Fertigstellung von Teilen des Programmsystems DIPOG zur Lösung direkter und inverser Probleme der klassischen Diffraktion bei binären und Multilevel-Gittern:

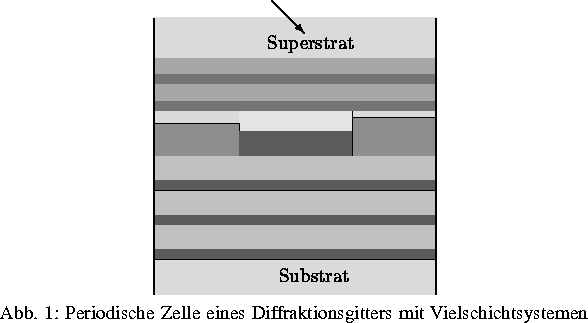
Auf der Basis der Ergebnisse der analytischen und numerischen Untersuchungen wurden verallgemeinerte FE-Methoden zur Berechnung von Beugungseffektivitäten von modernen Diffraktionsgittern auf Multilayer-Systemen implementiert. Der Querschnitt eines solchen Diffraktionsgitters ist in Abb. 1 dargestellt. Durch eine geeignete Wahl der optischen Indizes lassen sich eine Vielzahl der heute technologisch relevanten binären und Multilevel-Gitterformen realisieren.

Mit den implementierten Methoden lassen sich parallel die zur Gradientenberechnung benötigten direkten und dualen Probleme lösen, und somit können effektive Algorithmen zur Minimabestimmung von Zielfunktionen für das optimale Design-Problem entwickelt werden. Nach umfangreichen numerischen Tests wurden in Zusammenarbeit mit R. Henrion drei verschiedene auf Gradientenverfahren beruhende Algorithmen implementiert, die für beschichtete binäre Gitter u. a. vorgegebene Intensitätsverläufe über einem Bereich von Wellenlängen oder Einfallswinkeln optimieren bzw. Phasendifferenzen zwischen den TE- und TM-Polarisationen realisieren. Diese Teile des Programmsystems DIPOG werden beim Partner BIFO u. a. zur Simulation und zum Entwurf von Mikrooptiken in Hochleistungslasern, von HR-Spiegeln und Polarisationsschaltern eingesetzt (siehe z. B. [4]).

3. Analytische Untersuchungen des Problems der konischen Diffraktion an Gittern mit stückweise glatten Profilen:

Bei der konischen Diffraktion wird eine einfallende ebene Welle

$$\vec{E^i} = \vec{s} \exp(i \vec{k_0} \, \vec{r}) \exp(i \ome... ...ha, - \beta, \gamma )\; , \; k_0^2 = \omega^2 \epsilon_0 \mu_0$$

mit $\gamma \neq 0$ durch eine periodische und bezüglich der z-Richtung invariante diffraktive Struktur gebeugt; die Wellenvektoren der gebeugten Ordnungen liegen dann auf einem Konus.

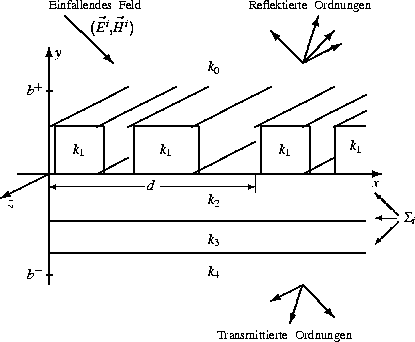
Abb. 1: Konische Diffraktion an einem binären Gitter

Das Gesamtfeld erfüllt die zeitharmonischen Maxwellschen Gleichungen

$$\begin{eqnarray*} \quad \nabla \times \vec{E} - i \omega \mu \vec{H} = 0 \; , \quad \nabla \times \vec{H} + i \omega \epsilon \vec{E} = 0 \end{eqnarray*}$$

mit den bekannten Stetigkeitsbedingungen an den Materialgrenzen

$$\hspace*{5mm} n \times [\vec{E}]=0 \; , \; n \times [\vec{H}]=0 \quad \mbox{auf} \; \Sigma_i$$

sowie Ausstrahlungsbedingungen im Unendlichen.

Die numerische Simulation der Beugungseffekte bei schrägem Einfall des Lichts spielt insbesondere für die Qualitätskontrolle von Beugungsgittern eine große Rolle. Es existieren von Ingenieuren entwickelte numerische Verfahren auf der Basis von Reihenentwicklungen, deren Konvergenz wegen der Lösungssingularitäten allerdings nicht abgesichert ist. In [5] wird gezeigt, daß die konische Diffraktion in ein zweidimensionales Problem überführt werden kann. Die Lösung $(\vec{E},\vec{H})$ kann aus den z-Komponenten

$$\quad E_z=u(x,y) \exp(i \alpha x+i \gamma z) \; , \quad \quad H_z=v(x,y) \exp(i \alpha x+i \gamma z)$$

bestimmt werden, wobei u und v H¹-Lösungen des Transmissionsproblems für die Helmholtz-Gleichungen

$$\quad \nabla_\alpha^2 u +(k^2-\gamma^2) u = 0 \; , \quad \quad \nabla_\alpha^2 v +(k^2-\gamma^2) v = 0$$

in dem Rechteck $[0,d] \times [b^-,b^+]$ sind, die die gekoppelten Sprungbedingungen

$$\left[ \frac{k^2 \, \partial_n^\alpha u}{k^2-\gamma^2} \righ... ...c{\partial_{\tau}^\alpha u }{k^2-\gamma^2} \right] _{\Sigma_i}$$

an den Materialgrenzen $\Sigma_i$ erfüllen. Hierbei bezeichnet

$$\nabla_\alpha := (\partial_x + i \alpha,\partial_y) \; , \; ... ...n) \; , \; \partial^\alpha_{\tau} := ( \nabla_\alpha,\tau) \; .$$

In [5] wird eine Variationsformulierung des Problems angegeben, mit deren Hilfe erstmals weitreichende Existenz- und Eindeutigkeitsaussagen für die konische Diffraktion bewiesen wurden. Es wird u. a. gezeigt, daß für physikalisch relevante Gittermaterialien die Variationsformulierung immer stark elliptisch ist und damit Stabilität von FE-Methoden vorliegt. Des weiteren wird bewiesen, daß für alle Frequenzen eindeutig bestimmte H¹-Lösungen existieren, wenn der optische Index mindestens eines Materials nicht reell ist. Außerdem werden die Singularitäten der Lösungen in den Interface-Ecken bestimmt. Daraus ergibt sich, daß im allgemeinen die Lösungen der Maxwellschen Gleichungen mit endlicher Energie keine quadratisch integrierbaren Gradienten besitzen.

Projektliteratur:

1.   G. BAO, D. DOBSON, J. COX, Mathematical studies in rigorous grating theory, J. Opt. Soc. Amer. A, 10, (1995) pp. 1029-1042.
2.   J. ELSCHNER, G. SCHMIDT, Periodic Structures and Optimal Design of Binary Gratings. I. Direct Problems and Gradient Formulas, erscheint in: Math. Meth. Appl. Sci.
3.   J. ELSCHNER, G. SCHMIDT, A rigorous numerical method for the optimal design of binary gratings, WIAS-Preprint No. 376 (1997), erscheint in: J. Modern Opt.
4.   H.-J. ROSTALSKI, J. GUHR, B. KLEEMANN, J. ELSCHNER, G. SCHMIDT, M. FERSTL, E. PAWLOWSKI, R. STEINGRÜBER, G. BOSTANJOGLO, R. MOTZKUS, Use of a multilayer dielectric diffraction grating as resonator mirror of a Nd:YAG laser, erscheint in: J. Modern Opt.
5.  J. ELSCHNER, R. HINDER, F. PENZEL, G. SCHMIDT, Existence, uniqueness and regularity for solutions of the conical diffraction problem, WIAS-Preprint, in Vorbereitung.