Simulation von monolithisch integrierten Höchstfrequenzschaltungen

Bearbeiter: G. Hebermehl , R. Schlundt  

Kooperation: W. Bruns, W. Heinrich, H. Zscheile (Ferdinand-Braun-Institut für Höchstfrequenztechnik), K. Beilenhoff, H. Klingbeil (TH Darmstadt)

Beschreibung der Forschungsarbeit: Die Arbeiten zur Simulation monolithisch integrierter Schaltungen für die Mikrowellentechnik wurden fortgesetzt. Die feldtheoretisch orientierten Methoden gehen von der dreidimensionalen Geometrie und den Materialeigenschaften aus und ermöglichen daher eine große Flexibilität bezüglich der analysierbaren Strukturen.

Die Entwicklung der Arbeiten wird durch den wachsenden Markt für die Mobilkommunikation und Sensortechnik bestimmt. Der hohe numerische Aufwand für die Simulation von Multichip-Aufbauten erfordert weiterhin verbesserte, kostengünstige und akkurat arbeitende Entwurfswerkzeuge für die Schaltungen.

Modellerweiterungen und die effektive Lösung von Aufgaben der linearen Algebra für hochdimensionale reelle und komplexwertige Matrizen stehen im Mittelpunkt.

Die Höchstfrequenzschaltungen werden als Verbindung unendlich langer, longitudinal homogener Wellenleiter mit einer Diskontinuität (siehe /home/unix/parnum/schlundt/tex/f3dgrid_22.eps) beschrieben. Die Eigenschaften der Schaltungen werden durch die Streumatrix widergespiegelt, die aus dem elektromagnetischen Feld berechnet wird. Das elektromagnetische Feld wird durch die Lösung eines dreidimensionalen Randwertproblems für die Integralform der Maxwellschen Gleichungen mit Wellenleiter-Randbedingung gewonnen. Durch die Verwendung der Maxwellschen Gleichungen im Frequenzbereich wird im Unterschied zu Zeitbereichsverfahren Modentrennung erreicht. Durch die Erweiterung des Modells auf verlustbehaftete Medien können einerseits Materialeigenschaften differenzierter berücksichtigt werden und andererseits für offene Strukturen PML-Randbedingungen (Perfectly Matched Layer) für die Absorption elektromagnetischer Wellen angegeben werden, indem bei der Formulierung der Maxwellschen Gleichungen ,,magnetische Ladungen und Ströme`` eingeführt werden:

$$\begin{array} {lllllll} \displaystyle{\oint_{\partial \Omega... ...vec \Omega} & \displaystyle{=} & \displaystyle{0} .\end{array}$$

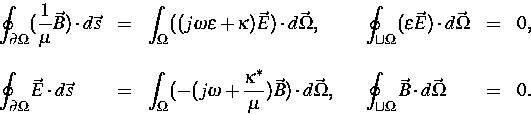
Die Diskretisierung der Gleichungen erfolgt mit Hilfe einer Finite-Volumen-Methode unter Verwendung eines kartesischen Gitters mit variabler Schrittweite und führt auf sehr rechenzeit- und speicherplatzaufwendige, z. T. auch schlecht konditionierte Eigenwertprobleme für schwach besetzte nichtsymmetrische oder nicht-Hermitesche Matrizen (verlustbehafteter Fall) und hochdimensionale lineare Gleichungssysteme mit schwach besetzten indefiniten symmetrischen oder symmetrischen komplexen Koeffizientenmatrizen. Die Lösungen der Eigenwertprobleme liefern die Randbedingungen an den Toren (Wellenleiter-Randbedingung) für das dreidimensionale Randwertproblem für die Diskontinuität.

Berechnung der Eigenmoden
Durch die Vermeidung der Berechnung aller Eigenwerte zur Bestimmung einer kleinen Menge von Ausbreitungskonstanten, die auf den komplexen Fall ausgedehnt werden konnte, und die damit mögliche Verwendung der Sparse-Matrix-Technik sowie durch die Vernachlässigung kleiner Elemente können jetzt Aufgaben, für deren Berechnung sonst Tage benötigt wurden, in Minuten auf einer Workstation gelöst werden.

Randwertproblem
Durch die Verwendung von 4 verschiedenen Arten auf die Aufgabe zugeschnittener Vorkonditionierer (darunter die Aufspaltung der hochdimensionalen Gleichungssysteme (3*10⁶ Unbekannte) mit Hilfe graphentheoretischer Methoden) in Zusammenhang mit Krylov-Verfahren werden erhebliche Verbesserungen in der Rechenzeit erreicht. Da die hochdimensionalen Gleichungssysteme i. allg. für mehrere rechte Seiten zu berechnen sind, wurden die Krylov-Verfahren für den Fall reeller Matrizen zur weiteren Steigerung der Effektivität auf diese Aufgabenstellung erweitert.

An der Lösung des dreidimensionalen Randwertproblems im verlustbehafteten Fall wird noch gearbeitet.

Die Ergebnisse der Forschungsarbeiten wurden in den Publikationen [3, 4, 5, 6, 7, 8, 9] dargestellt.

Projektliteratur:

1.   K. BEILENHOFF, W. HEINRICH, H. L. HARTNAGEL, Improved Finite-Difference Formulation in Frequency Domain for Three-Dimensional Scattering Problems, IEEE Trans. Microwave Theory Tech., Vol. 40, No. 3 (1992), pp. 540-546.
2.   A. CHRIST, H. L. HARTNAGEL, Three-Dimensional Finite-Difference Method for the Analysis of Microwave-Device Embedding, IEEE Trans. Microwave Theory Tech., Vol. MTT-35, No. 8 (1987), pp. 688-696.
3.   G. HEBERMEHL, R. SCHLUNDT, H. ZSCHEILE, W. HEINRICH, Eigen mode solver for microwave transmission lines, WIAS-Preprint No. 308 (1997).
4.   , Eigen mode solver for microwave transmission lines, COMPEL, Vol. 16 (1997), No. 2, pp. 108-122.
5.   ,Improved numerical solutions for the simulation of microwave circuits, WIAS-Preprint No. 309 (1997).
6.   ,Improved numerical solutions for the simulation of microwave circuits, in: Progress in Industrial Mathematics at ECMI 96, (M. Brøns, M. Ph. Bendsøe, M. P. Sørensen, eds.) B. G. Teubner, Stuttgart (1997), pp. 176-183.
7.   ,Numerical solutions for the simulation of monolithic microwave integrated circuits, WIAS-Preprint No. 316 (1997), eingereicht bei: SIAM J. Sci. Comput., 1997.
8.   ,Improved numerical methods for the simulation of microwave circuits, WIAS-Preprint No. 378 (1997), eingereicht bei: Surveys Math. Indust., 1997.
9.  G. HEBERMEHL, Eigen mode solver for monolithic integrated circuits, in: Abstracts ENUMATH 1997, Second European Conference on Numerical Mathematics and Advanced Applications, Ruprecht-Karls-Universität Heidelberg (1997), pp. 244-245.