Intermittierende Dynamik

Bearbeiter: F. Guyard , R. Lauterbach  

Kooperation: P. Chossat (Institut Non Linéaire de Nice, Nizza), E. Bänsch (Universität Tübingen)

Förderung: DFG: Schwerpunktprogramm ,,Ergodentheorie, Analysis und effiziente Simulation dynamischer Systeme``, DAAD: PROCOPE

Beschreibung der Forschungsarbeit:

In einer Arbeit der Stuttgarter Physiker Friedrich und Haken [2] wurde intermittierende Dynamik im sphärischen Bénard-Problem numerisch festgestellt. In ergänzenden Untersuchungen [1] zu einer früheren Arbeit wurde ein ähnliches Verhalten analytisch nachgewiesen.

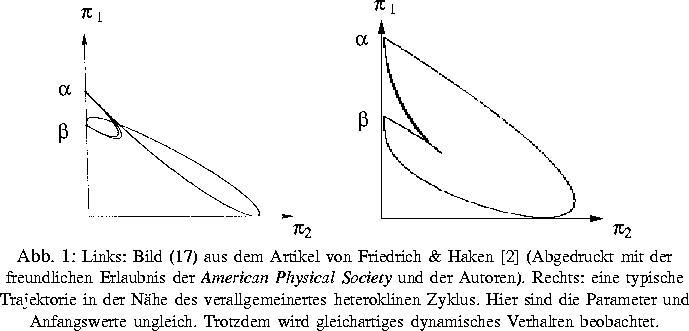
Insbesondere konnte gezeigt werden [1], daß dieses Verhalten bei langsamer Rotation erhalten bleibt. Damit wurde zum ersten Mal ein analytischer Zugang zum Problem der Polwechsel des Erdmagnetfeldes bei langsamer Rotation entwickelt. Natürlich kann dies nur ein erster Schritt auf dem Weg zum Verständnis dieses Verhaltens sein.

Weitere Untersuchungen, die dazu dienen, unser sehr einfaches Modell näher an die Wirklichkeit heranzuführen, wurden begonnen:

1.

Untersuchungen zur schnellen Rotation: neue Symmetrieeigenschaften, Bestimmung der Darstellungen, Reduktion der Gleichung.

2.

Untersuchung von Effekten der Solidifikation am Kern als Energiequelle.

3.

Direkte numerische Simulation der Navier-Stokes-Gleichungen zur Überprüfung der analytisch vorhergesagten Resultate. Dabei zeichnet sich ab, daß Eigenschaften des Gitters qualitative Eigenschaften der errechneten Lösungen bestimmen.

4.

Beginn von Arbeiten, um dieses Phänomen in einfacheren Gleichungen aufzuzeigen. Diese einfacheren Gleichungen sind Systeme von Reaktions-Diffusionsgleichungen. Um diese Frage systematisch zu untersuchen, wird die numerische Näherung als diskretes, endlich-dimensionales System aufgefaßt. Orbital stabile Mannigfaltigkeiten von Lösungen treten als normal hyperbolische Mannigfaltigkeiten dieser endlich-dimensionalen Systeme auf. Damit wird die Theorie der erzwungenen Symmetriebrechung [3,4,5], die in den letzten Jahren entwickelt wurde, anwendbar. Diese sagt, abhängig von der Symmetrie der Störung (und des Symmetrietyps der zu berechnenden Lösung) ein dynamisches Verhalten voraus, das entweder aus Drift längs der Mannigfaltigkeit oder an einer endlichen Anzahl von hyperbolischen Gleichgewichten besteht. Während für den zweiten Fall leicht Gitter angegeben werden können, die dieses Verhalten zeigen, ist es unklar, ob der erste Fall überhaupt in einer numerischen Näherung eintreten kann. Unabhängig davon ist es wichtig herauszufinden, welche numerisch beobachteten Symmetrieeigenschaften tatsächlich auftreten. Alle genannten Aspekte bedürfen weiterer Untersuchungen.

Projektliteratur:

1.  P. CHOSSAT, F. GUYARD, R. LAUTERBACH, Generalized heteroclinic cycles in spherically invariant systems and their perturbations, WIAS-Preprint No. 303, 1996 (revidierte Version Sept. 1997, erscheint in: J. Nonlinear Sci.).
2.  R. FRIEDRICH, H. HAKEN, Static, wavelike, and chaotic thermal convection in spherical geometries, Phys. Rev. A, 34 (1986), pp. 2100-2120.
3.  F. GUYARD, R. LAUTERBACH, Forced symmetry breaking for periodic solutions, Nonlinearity, 10 (1997), pp. 291-310.
4.  R. LAUTERBACH, M. ROBERTS, Heteroclinic cycles in dynamical systems with broken spherical symmetry, J. Differential Equations, 100 (1992), pp. 428-448.
5.  S. MAIER-PAAPE, R. LAUTERBACH, Reaction diffusion systems on the 2-sphere and forced symmetry breaking, WIAS-Preprint No. 173, 1995, erscheint in: Trans. Amer. Math. Soc.