Optimale Steuerung diskontinuierlicher Destillationsprozesse

Bearbeiter: I. Bremer , M. Hanke , K. R. Schneider  

Kooperation: B. Hegner (BASF AG, Ludwigshafen), G. Wozny (TU Berlin)

Beschreibung der Forschungsarbeit: Die ökonomische Bedeutung der Batchdestillation, ihre mathematische Modellierung sowie das Konzept zu ihrer optimalen Steuerung wurden in den Forschungsberichten der beiden letzten Jahre dargestellt. JFB 95 JFB 96 Im Mittelpunkt der Untersuchungen im Berichtszeitraum standen folgende Fragen

1.

Verbesserung der Schrittweitensteuerung,

2.

Implementierung der internen Differentiation,

3.

Verwendung stochastischer Verfahren (Simulated Annealing) zur Ermittlung zulässiger Startlösungen für die Optimierung.

Im Berichtszeitraum wurde eine Variante der Black-Box-Optimierung implementiert und an die BASF AG übergeben. Sie basiert auf der Verwendung eines lokal konvergenten Optimierungsverfahrens (SQP). Bei ihrem Einsatz treten folgende Probleme auf:

1.

Die Berechnung zulässiger Steuerungen, d. h. Steuerungen, die die Einhaltung aller Nebenbedingungen (insbesondere auch Reinheits- und Sicherheitsbedingungen) gewährleisten, kann sehr aufwendig sein.

2.

Die Verwendung numerisch berechneter Gradienten wirkt sich insbesondere in der Umgebung des zu berechnenden Optimums negativ aus.

3.

Die berechneten Optima sind lokal.

Um die in (ii) genannten Nachteile zu beseitigen, wurde der Simulator der BASF um die Möglichkeit zur Berechnung der analytischen Gradienten mittels interner Differentiation ergänzt. Nach übereinstimmender Ansicht der Projektpartner stellt eine erfolgreiche Lösung des in (i) beschriebenen Problems einen wesentlichen Schritt zur Lösung des Gesamtproblems dar. 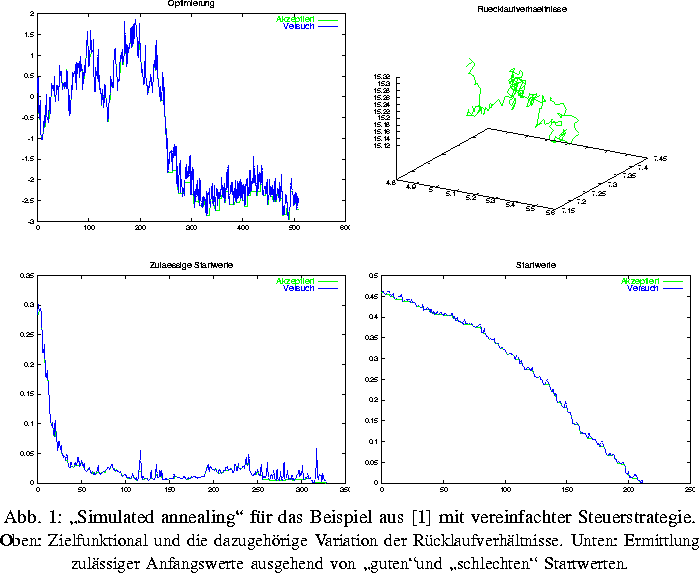Als alternative Möglichkeit zur Behandlung dieses Problems, aber auch zur Überwindung der in (ii) und (iii) genannten Probleme, wurden Untersuchungen zu stochastischen Optimierungsmethoden vorgenommen, die auf der Methode des ,,Simulierten Annealing`` beruhen.

Simulated Annealing.

Hierzu müssen übliche Simulatoren für Batch-Prozesse nicht verändert werden, da sie nur als Black-Box-Programm zur Berechnung von Kostenfunktionalen benutzt werden. Die Erfahrungen mit Beispielen aus der Literatur und realen Modellen sowie mit verschiedenen Simulatoren zeigen, daß das Problem (i) damit zufriedenstellend gelöst werden kann. Da das Verfahren ableitungsfrei ist, ist Problem (ii) nicht relevant. Bei geeigneten Annealing-Strategien konvergiert das Verfahren (in Wahrscheinlichkeit) gegen ein globales Minimum. Allerdings ist die Konvergenz recht langsam. Daher soll die geeignete Kopplung des stochastischen Verfahrens mit überlinear konvergenten Verfahren weiter untersucht werden.

Interne Differentiation.

    $$\begin{eqnarray} & \begin{array} {ccl} {\displaystyle \frac{dx^{(1)}}{dt}}&=&f_1... ..._u+ \frac{\partial f_2}{\partial u}(x^{(1)},x^{(2)},u).\end{array}\end{eqnarray}$$

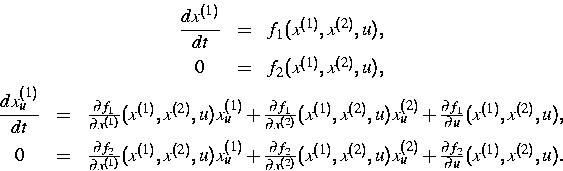
Im wesentlichen wird das dem Modell zugrundeliegende DAE-System (1) um die entsprechenden linearisierten Gleichungssysteme (2) ergänzt und synchron zum Ausgangssystem mitbehandelt, so daß sich (abgesehen von Rundungsfehlern) der exakte analytische Gradient für die Ausdrücke, die zur Berechnung des Zielfunktionals und der Nebenbedingungen nötig sind, ergibt (siehe JFB 96 ). Der Effekt zeigt sich zum einen im verringerten CPU-Zeitaufwand für die Berechnung von Funktional und Gradient, zum anderen in einem wesentlich glatteren Verlauf und besserer Konvergenz des SQP-Verfahrens (siehe Tabelle 1).

Gradient Anzahl Anz. Iter. f. Anz. Iter. f. berechnetes CPU-Zeit

Simulationsl. zul. Startwerte Optimierung Optimum

analytisch 10 3 6 2.6237 243.54 s

numerisch 33 + 20*6 3 17 2.5961 1430.01 s

Bei der Verwendung der internen Differentiation sind folgende technische Besonderheiten zu beachten:

• Zeitpunkte können nicht direkt als Parameter angegeben werden, sondern nur über den Umweg der Zeittransformation des jeweiligen Intervalls.
• Um ein konvergentes Verfahren zu erhalten, muß in der Nähe des Optimums die Zeitdiskretisierung im Simulator konstant bleiben.
• Zustandsabhängige Definitionen der Länge von Zeitintervallen für Zielfunktional und Nebenbedingungen müssen jeweils umformuliert werden als ein zusätzlicher Zeitparameter und eine zusätzliche Nebenbedingung für die Optimierung, die den zu erreichenden Zustand beschreibt.

Projektliteratur:

1.   P. LI, G. WOZNY, Dynamische Optimierung großer chemischer Prozesse mit Kollokationsverfahren am Beispiel Batch-Destillation, Automatisierungstechnik, 45 (1997) 3, pp. 136-149.
2.   VL. KVASNICKA, J. POSPICHAL, Simulated Annealing, Matcdy, 34 (1996), pp. 7-49.
3.   H.E. ROMEIJIN, R.L. SMITH, Simulated Annealing for constrained global optimization, J. Glob. Optim., 5 (1994), pp. 101-126.