Phasenfeldgleichungen und Stefan-Probleme

Bearbeiter: O. Klein , J. Sprekels  

Kooperation: P. Colli (Universität Pavia), C. Verdi (Universität Mailand)

Förderung: EU, ESF/FBP Research Fellowship

Beschreibung der Forschungsarbeit:

Die Modellierung von diffusiven Phasenübergängen, wie z. B. des Kristallwachstums, mit Phasenfeldgleichungen vom Penrose-Fife-Typ führt zu Systemen der Form  

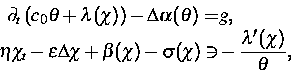$$\begin{split} \partial_t\left(c_0 \theta + \lambda(\chi)\rig... ... \sigma(\chi) \ni& - \frac{\lambda'(\chi)}{\theta},\end{split}$$ (1)

wobei $\beta$ ein maximal monotoner Graph ist. Dieses System beschreibt die Entwicklung der absoluten Temperatur $\theta$und des Ordungsparameters $\chi$.Das Projekt ist eine Fortführung aus den Vorjahren.

a) Für dieses System werden Semidiskretisierungen in der Zeit betrachtet. Hierbei ist $\eta$ eine vom Ort abhängige positive Funktion, und $\alpha(\theta) =-\kappa / \theta$,d. h. der Wärmefluß ist proportional zum Gradienten der inversen Temperatur.

Im Berichtszeitraum sind die Arbeiten an der Dissertation [5] abgeschlossen worden, in der eine Semidiskretisierung von (1) für lineares $\lambda$ und $\sigma$ betrachtet wird. In dieser Arbeit wird Konvergenz gegen die Lösung des Penrose-Fife-Systems, verschiedener Stefan-Probleme (vgl. auch [4]), und eines degenerierten Penrose-Fife-Systems, bei dem $\eta$ auf einer Menge mit positivem Maß verschwindet, bewiesen.

Für allgemeineres $\lambda$ und $\phi$ wird in [6] eine Semidiskretisierung in der Zeit vorgestellt und Konvergenz hergeleitet. Dabei gelang es, durch Verwendung von Resultaten aus [7] zu zeigen, daß der Fehler der zeitlichen Diskretisierung linear in der Zeitschrittweite h ist, während in [4,5] nur eine Fehlerabschätzung der Ordnung $\sqrt{h}$ hergeleitet wurde.

b) In [1] wurde die Existenz und Eindeutigkeit einer globalen eindeutigen Lösung für das Penrose-Fife-System in Fällen nachgewiesen, in denen $\alpha$ nicht von der Form $\alpha(\theta) =-\kappa / \theta$ ist, wobei es allerdings weiterhin notwendig war, für $\alpha$ eine Singularität in 0 vorauszusetzen. Wenn der Wärmefluß dem Fourier'schen Gesetz entspricht, ist $\alpha(\theta)= \kappa \theta$ und somit dieses Resultat nicht anwendbar. Für das Penrose-Fife-System mit Fourier'schem Wärmefluß konnte in [3] erstmalig Existenz und Eindeutigkeit einer globalen Lösung bewiesen werden; dieses Resultat ist auf den Fall $\,\varepsilon = 0\,$ beschränkt, d. h. wenn keine Grenzflächenenergie berücksichtigt wird.

Das Thema wurde im Rahmen des EU-Projektes ,,Phase Transition and Surface Tension`` bearbeitet.

Projektliteratur:

1.   P. COLLI, PH. LAURENCOT, J. SPREKELS, Global solution to the Penrose-Fife phase-field model with special heat flux law, erscheint in: Proceedings of the IUTAM-Conference in Paris, April 1997.
2.   P. COLLI, J. SPREKELS, Stefan problems and the Penrose-Fife phase field model, Adv. Math. Sci. Appl., Vol. 7 (1997), pp. 911-934.
3.  , Global solution to the Penrose-Fife phase field model with zero interfacial energy and Fourier law, erscheint in: Adv. Math. Sci. Appl.
4.   O. KLEIN, A semidiscrete scheme for a Penrose-Fife system and some Stefan problems in $\IR^3$, Adv. Math. Sci. Appl., Vol. 7 (1997), pp. 491-523.
5.  , Existence and Approximation Results for Phase-Field Systems of Penrose-Fife Type and Stefan Problems, Dissertation, Humboldt-Universität zu Berlin, ISBN 3-8265-3056-X.
6.  , Existence and approximation results for Penrose-Fife systems, in Vorbereitung.
7.   R. H. NOCHETTO, G. SAVAR´E, C. VERDI, A posteriori error estimates for variable time-step discretizations of nonlinear evolution equations, in Vorbereitung.
8.  O. PENROSE, P. C. FIFE, Thermodynamically consistent models of phase-field type for the kinetics of phase transitions. Physica D, 43 (1990), pp. 44-62.