




Next: Phasenfeldgleichungen und Stefan-Probleme
Up: Projektbeschreibungen
Previous: Elektro-Reaktions-Diffusionsgleichungen in Heterostrukturen mit Anwendungen in
Bearbeiter: H.-Chr. Kaiser
,
J. Rehberg
Beschreibung der Forschungsarbeit:
Die Arbeit des Jahres 1997 am Kohn-Sham-System setzte die des
Jahres 1996 konsequent fort. Insbesondere ging es darum, für das
räumlich eindimensionale System, das Quantum-Wells
- den in der Physik und Technik häufigsten Fall von
dimensionsreduzierten Halbleiterstrukturen -
beschreibt, Existenz- und Regularitätsaussagen herzuleiten
(vgl. WIAS-Preprint No. 368, 1997), die denen der zwei- und dreidimensionalen Probleme mit
Austausch-Korrelations-Potential entsprechen
(vgl. WIAS-Preprint No. 339, 1997). Die Schwierigkeit lag hierbei darin, daß der
Austausch-Korrelationsterm im räumlich eindimensionalen Fall
nicht mehr durch eine stetige Abbildung von L1 nach L2
dargestellt werden kann, sondern die durch ihn
definierten Potentiale nur noch als in L1 liegend angenommen werden
können.
Indessen erwies es sich, daß die L1-Potentiale im Sinne der
Störungstheorie von Formen noch behandelt werden können, und daß
die Birman-Solomyak-Techniken, welche Abschätzungen der Lösungen
in Termen der Daten des Problems ermöglichen, noch anwendbar sind.
Ein zweiter Arbeitsschwerpunkt des Jahres 1997 lag in der
Konzeption von Modellen, die auf eine Einbettung der
quantenmechanischen Beschreibung der Nanostruktur in eine
makroskopische Beschreibung der Umgebung hinzielen.
Es handelt sich hierbei um ein äußerst kompliziertes Problem, das
in den letzten Jahren in den Blickwinkel sowohl der Mathematik
als auch Physik geriet und von einer befriedigenden Lösung
noch sehr weit entfernt zu sein scheint (vgl. [2]).
Wir streben bezüglich dieses Problems keine
universelle Lösung im Sinne von First Principles an
(vgl. dazu z. B.
[4] und die
dort zitierten Arbeiten in diese Richtung),
sondern es soll ein phänomenologisches Modell erstellt werden,
welches eine selbstkonsistente Kopplung des bewährten
van Roosbroeck-Systems zur elektronischen Modellierung von
Halbleitermikrostrukturen mit dem Kohn-Sham-System zur
Beschreibung von Nanostrukturen darin,
wie etwa eingebetteten Quantum-Wells oder -Wires,
realisiert (vgl. [3]).
Ausgangspunkt unserer Überlegungen war die Beobachtung
(vgl. WIAS-Preprint No. 339, 1997), daß im Fall des bisher betrachteten
Kohn-Sham-Systems mit selbstadjungiertem Hamiltonian
nicht nur die quantenmechanische Stromdichte über der gesamten
Nanostruktur verschwindet, sondern auf dem Rand der Struktur
selbst die Normalenableitung der Teilchendichte.
Im allgemeinen wird dadurch die Stromkontinuität verletzt,
und die numerische Simulation mit so einfach aneinandergefügten
van Roosbroeck- und Kohn-Sham-Systemen scheitert daran
(vgl. hierzu z. B. die entsprechenden Versuche von P. Ellrodt
[1]).
Die Stromkontinuität wurde nun bei uns an die Spitze der Überlegungen
gestellt:
das Zusammenfügen der beiden Modelle sollte so geschehen, daß
am Interface der verschieden modellierten Halbleitergebiete
sowohl die mikroskopischen und makroskopischen Teilchendichten als
auch die Normalkomponenten der entsprechenden Ströme stetig
ineinander übergehen.
Ausgangspunkt war, zunächst im Fall eines nicht-selbstadjungierten
Hamiltonian mit ausschließlich einfachen (normierten) Eigenelementen
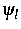 ,eine korrespondierende Definition von Teilchendichten und -strömen
in der Nanostruktur durch gewichtete Summen:
,eine korrespondierende Definition von Teilchendichten und -strömen
in der Nanostruktur durch gewichtete Summen:
![\begin{displaymath}
u\;=\; \sum_l N_l\;\big\vert\psi_l\big\vert^2
\qquad
j\;=\; \sum_l N_l\; \Im\big[\psi_l^*\nabla\psi_l\big]
.\end{displaymath}](../../1997/html/images/img96.gif)
Die Nl sind dabei wie im selbstadjungierten Fall reelle
Besetzungsfaktoren, deren genaue Form noch geklärt werden muß.
Versieht man einen Kohn-Sham-Hamiltonian mit der unsymmetrischen (!)
Randbedingung
| 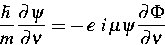 |
(1) |
auf dem Interface zwischen der Nanostruktur und dem übrigen durch das
van Roosbroeck-System beschriebene elektronische Bauelement, so
folgt die Stromkontinuität, wenn man die Stetigkeit der
Teilchendichten gewährleistet.
Dabei ist
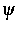 eine beliebige Eigenfunktion,
m die effektive Masse,
eine beliebige Eigenfunktion,
m die effektive Masse,
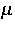 die Beweglichkeit,
die Beweglichkeit,
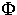 das makroskopische Quasi-Fermi-Potential
und
das makroskopische Quasi-Fermi-Potential
und 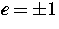 die Ladung der betrachteten Ladungsträger
sowie
die Ladung der betrachteten Ladungsträger
sowie 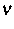 der äußere Normaleneinheitsvektor auf dem
Rand der Nanostruktur.
Da man die Stetigkeit der Teilchendichten am Interface zwischen
dem Kohn-Sham- und dem van Roosbroeck-System durch eine geeignete
Randbedingung an die Stromkontinuitätsgleichung im
van Roosbroeck-System sichern kann, war die vorstehende Beobachtung
Anlaß, den nicht-selbstadjungierten Hamiltonian mit der Randbedingung
(*) genauer zu betrachten.
Unter sinnvollen Annahmen über das makroskopische
Quasi-Fermi-Potential
der äußere Normaleneinheitsvektor auf dem
Rand der Nanostruktur.
Da man die Stetigkeit der Teilchendichten am Interface zwischen
dem Kohn-Sham- und dem van Roosbroeck-System durch eine geeignete
Randbedingung an die Stromkontinuitätsgleichung im
van Roosbroeck-System sichern kann, war die vorstehende Beobachtung
Anlaß, den nicht-selbstadjungierten Hamiltonian mit der Randbedingung
(*) genauer zu betrachten.
Unter sinnvollen Annahmen über das makroskopische
Quasi-Fermi-Potential 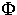 ist
ist
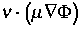 eine auf dem Rand der Nanostruktur konzentrierte Distribution
und erlaubt, die formale Randbedingung (*) als
quadratische Form auf L2 zu definieren.
Diese (unsymmetrische) Randform ist infinitesimal klein gegen die
Form des reinen Differentialoperators im Hamiltonian.
Mit Hilfe der Störungstheorie von Formen kann
gezeigt werden, daß es genau einen Hamiltonoperator H mit der
Randbedingung (*) auf L2 gibt.
Dieser ist zwar unsymmetrisch, erzeugt
aber auf L2 eine analytische Halbgruppe.
Darüber hinaus hat H eine kompakte Resolvente, die der gleichen
Summierbarkeitsklasse angehört wie die Resolvente
des Laplace-Operators mit homogenen Neumannschen Randbedingungen.
H besitzt ein in H1 vollständiges System von
Wurzelvektoren und hat im wesentlichen dieselbe
Spektral-Asymptotik wie der Operator ohne Randanteil.
Obwohl die von uns betrachteten nicht-selbstadjungierten
Hamiltonoperatoren im Kohn-Sham-System generisch nur einfache
Eigenelemente besitzen, ist eine allgemeingültige Definition der
Teilchen- und Stromdichte noch erforderlich, genauso wie die
Klärung der Besetzungsstatistik.
Weiterhin werden wir uns mit der Wechselwirkung des
van Roosbroeck-Systems mit dem Kohn-Sham-System
in Blick auf a priori-Abschätzungen, Existenz und
Einzigkeit für das selbstkonsistent gekoppelte Gesamtsystem
befassen.
eine auf dem Rand der Nanostruktur konzentrierte Distribution
und erlaubt, die formale Randbedingung (*) als
quadratische Form auf L2 zu definieren.
Diese (unsymmetrische) Randform ist infinitesimal klein gegen die
Form des reinen Differentialoperators im Hamiltonian.
Mit Hilfe der Störungstheorie von Formen kann
gezeigt werden, daß es genau einen Hamiltonoperator H mit der
Randbedingung (*) auf L2 gibt.
Dieser ist zwar unsymmetrisch, erzeugt
aber auf L2 eine analytische Halbgruppe.
Darüber hinaus hat H eine kompakte Resolvente, die der gleichen
Summierbarkeitsklasse angehört wie die Resolvente
des Laplace-Operators mit homogenen Neumannschen Randbedingungen.
H besitzt ein in H1 vollständiges System von
Wurzelvektoren und hat im wesentlichen dieselbe
Spektral-Asymptotik wie der Operator ohne Randanteil.
Obwohl die von uns betrachteten nicht-selbstadjungierten
Hamiltonoperatoren im Kohn-Sham-System generisch nur einfache
Eigenelemente besitzen, ist eine allgemeingültige Definition der
Teilchen- und Stromdichte noch erforderlich, genauso wie die
Klärung der Besetzungsstatistik.
Weiterhin werden wir uns mit der Wechselwirkung des
van Roosbroeck-Systems mit dem Kohn-Sham-System
in Blick auf a priori-Abschätzungen, Existenz und
Einzigkeit für das selbstkonsistent gekoppelte Gesamtsystem
befassen.
Projektliteratur:
- P. ELLRODT, Simulation of InAlAs/InGaAs dual gate HFET using a
2D and a Q2D model, in: Ninth III-V Semiconductor Device Simulation
Workshop, Eindhoven University of Technology, May 9 - 10, 1996, Eindhoven
University of Technology, May 1996.
- I. M. GAMBA, C. S. MORAWETZ, A viscous approximation for a
2-d steady semiconductor or transonic gas dynamic flow: Existence theorem
for potential flow, Comm. Pure Appl. Math., XLIX (1996),
pp. 999-1049.
- H.-CHR. KAISER, J. REHBERG, Matching the phenomenological and
the quantum mechanical description of semiconductor devices.
Workshop ,,Phase Transitions: Microscopic and Mesoscopic
Theory``, WIAS Berlin, 2-7 June , 1997.
- R. OLKIEWICZ, Some mathematical problems related to
classical-quantum interaction, Rev. Math. Phys., 9 (1997),
pp. 719-747.





Next: Phasenfeldgleichungen und Stefan-Probleme
Up: Projektbeschreibungen
Previous: Elektro-Reaktions-Diffusionsgleichungen in Heterostrukturen mit Anwendungen in
LaTeX typesetting by I. Bremer
1/18/1999
![]() ,eine korrespondierende Definition von Teilchendichten und -strömen
in der Nanostruktur durch gewichtete Summen:
,eine korrespondierende Definition von Teilchendichten und -strömen
in der Nanostruktur durch gewichtete Summen:
![]()