Elektro-Reaktions-Diffusionsgleichungen in Heterostrukturen mit Anwendungen in der Halbleitertechnologie

 Bearbeiter: R. Hünlich , A. Glitzky , W. Röpke  

Kooperation: B. Heinemann, F. Herzel, U. Jagdhold, H. Rücker u. a. (Institut für Halbleiterphysik Frankfurt (Oder) GmbH (IHP)), N. Strecker (Institut für Integrierte Systeme, ETH Zürich)

Förderung: BMBF

Beschreibung der Forschungsarbeit: Im inzwischen abgeschlossenen Vorhaben wurden Beiträge zur Modellierung und Simulation von Prozessen geleistet, die bei der Herstellung von Bauelementen der Nanoelektronik ablaufen (siehe [2,3]). Behandelt wurden Fragestellungen, die beim Verbundpartner, dem Institut für Halbleiterphysik Frankfurt(Oder), bei der Entwicklung von SiGe-Hetero-Bipolartransistoren im Rahmen des LOTUS-Projektes auftraten (siehe [4]).

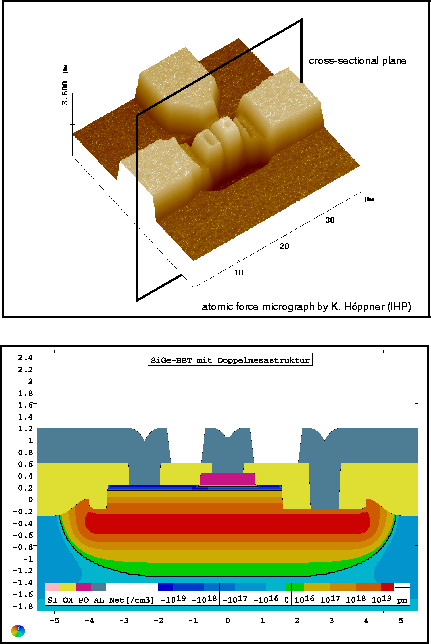
Aus Sicht der Anwendungen bestand das Anliegen des Vorhabens darin, die beim Verbundpartner eingesetzten Technologiesimulatoren (vgl. Abb. 1) entsprechend dem neuen Transistorkonzept weiterzuentwickeln. Schwerpunkte waren dabei Untersuchungen zur Diffusion von Bor (und anderen Fremdatomen) in verspannten SiGe-Schichten.

 


Das hierzu entwickelte, verifizierte und implementierte Modell (vgl. Abb. 2) hat sich grundsätzlich bewährt, muß aber für zukünftige Untersuchungen aus mehreren Gründen verbessert werden (siehe [3]). Einer der Gründe besteht darin, daß der Einfluß des inneren elektrischen Feldes an den Heterogrenzen genauer berücksichtigt werden sollte. Das elektrostatische Potential ist dann nicht mehr aus der Annahme der lokalen Elektroneutralität, sondern als Lösung einer nichtlinearen Poissongleichung mit einer nichtlokalen Nebenbedingung zu berechnen (siehe [3] sowie den Beitrag auf S. ). Etwas vereinfacht läßt sich dieses Problem wie folgt beschreiben:

$$-\lambda^2\,\nabla\cdot(\varepsilon_{\text{rel}}\nabla\Phi) + e_0(\Phi+\zeta)= u_0\quad\text{in } \Omega,$$

$$\Phi = 0 \quad\text{auf }\Gamma_D,\quad \lambda^2\,\nu\cdot(... ...ext{rel}}\nabla \Phi)+\tau \Phi = 0 \quad \text{auf } \Gamma_N$$

$$\int\limits_{\Omega}e_0(\Phi+\zeta) \,\text dx = \int\limits_{\Omega}u_0\,\text dx\,.$$

Zu bestimmen sind das elektrostatische Potential $\Phi$ und das elektrochemische Potential der Elektronen $\zeta$, die Dotierung u₀ ist vorgegeben. Ferner ist $e_0(y)=\overline ne^y-\overline pe^{-y}$; die materialabhängigen Größen $\varepsilon_{\text{rel}},\,\tau,\,\overline n,\,\overline p$ sind in Heterostrukturen bezüglich x unstetig. Die Elektronen- bzw. Löcherdichte erhält man dann gemäß

$$n=\overline ne^{\Phi+\zeta},\quad p=\overline pe^{-\Phi-\zeta}.$$

Zur Lösung dieser Aufgabe wurden 1D-Programme entwickelt, um die Unterschiede zur bisher benutzten lokalen Elektroneutralitätsnäherung zu klären. Ergebnisse für eine typische Si/SiGe/Si-Struktur sind in Abb. 3 dargestellt.

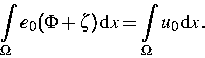
Gegenstand der analytischen und numerischen Untersuchungen waren Elektro-Reaktions-Diffusionsgleichungen, die relevante Aufgaben aus der Halbleitertechnologie modellieren. Zur Existenz, Einzigkeit und zum asymptotischen Verhalten von Lösungen dieser Gleichungen und ihrer semidiskreten Form wurden neue Resultate erzielt. Auf diese und weiterführende Ergebnisse wird im Beitrag auf S.  eingegangen.

 

 

Projektliteratur:

1.  F. HERZEL, K.-E. EHWALD, B. HEINEMANN, D. KRÜGER, R. KURPS, W. RÖPKE, H.-P. ZEINDL, Deconvolution of narrow boron SIMS depth profiles in Si and SiGe, Surface and Interface Analysis, 23 (1995), pp. 764-770.
2.  R. HÜNLICH, A. GLITZKY, J. GRIEPENTROG, W. RÖPKE, Zu einigen Fragen der Modellierung und Simulation bei der Entwicklung von SiGe-Heterojunction-Bipolartransistoren, in: Mathematik - Schlüsseltechnologie für die Zukunft (K.-H. Hoffmann, W. Jäger, Th. Lohmann, H. Schunck, Hrsg.), Springer-Verlag Berlin Heidelberg, 1997, pp. 303-313.
3.  R. HÜNLICH, A. GLITZKY, W. RÖPKE, Reaktions-Diffusionsgleichungen in Heterostrukturen mit Anwendungen in der Halbleitertechnologie. Schlußbericht zu einem Vorhaben im BMBF-Förderprogramm ,,Anwendungsorientierte Verbundvorhaben auf dem Gebiet der Mathematik``, WIAS-Report No. 13 (1997).
4.  Institut für Halbleiterphysik Frankfurt (Oder), Jahresforschungsbericht 1996.