Diffusion und Reaktion von Iod in aktiviertem Polyethylen

Bearbeiter: K. Zacharias  

Kooperation: G. Rafler, R. Wilken (Fraunhofer-Institut für Angewandte Polymerforschung, Teltow-Seehof)

Beschreibung der Forschungsarbeit: Bei Bestrahlung einer dünnen Polyethylenschicht mit ultraviolettem Licht geeigneter Wellenlänge entstehen freie Radikale. Zu ihrem Nachweis läßt man Iod in die Polymerschicht eindiffundieren. Das dabei in der Schicht entstehende Iodid kann - bis zu einer gewissen Analysentiefe - durch XPS-Messungen (X-ray Photoelectron Spectroscopy) ermittelt werden. Zur quantitativen Untersuchung dieses Vorgangs wird ein Reaktions-Diffusionsmodell zur Beschreibung der Reaktion freier Radikale mit eindiffundierendem Iod betrachtet. Bei der mathematischen Modellierung werden Reaktionskinetik und Transport des Iods durch Diffusion berücksichtigt. Das mathematische Modell besteht demgemäß aus einer Kombination von Reaktionsgleichungen mit einer Diffusions-Reaktionsgleichung. Das Modell soll Aussagen über den Einfluß der beteiligten Parameter (Diffusionskonstante, Geschwindigkeitskonstanten, Konzentration des Iods am Rand und Anfangskonzentration der Radikale) liefern. Durch Vergleich mit vorliegenden Messungen soll die Richtigkeit der dem Modell zugrunde gelegten Vorstellungen überprüft werden. Das Modell wurde von Herrn R. Wilken (IAP Teltow-Seehof) vorgeschlagen.

Die beteiligten Substanzen (bzw. deren Konzentrationen) seien $\;I\;$ - Iod, $\;R\;$ - Radikale, $\;S\;$ - Iodid.

Die experimentellen Gegebenheiten gestatten es, ein räumlich eindimensionales Modell zu betrachten. Demgemäß werden Konzentrationsverläufe

$$\begin{eqnarray*} I = I(t,x),\quad R = R(t,x),\quad S = S(t,x)\end{eqnarray*}$$

auf dem Gebiet

$$G = \{(t,x):\;0 < t < T,\;0<x<a\}$$

gesucht, die dort folgenden Gleichungen genügen:

$$\frac{\partial I}{\partial t} = D\frac{{\partial}^2 I} {\partial x^2} - c_1IR,$$ (1)

$$\!\frac{dR}{dt} = - c_1IR - c_2R ,$$ (2)

$$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\frac{dS}{dt} = c_1IR .$$ (3)

Für die Iodkonzentration sind Randbedingungen

$$I(t,0)=I_0,\quad \frac{\partial I}{\partial x}(t,a)=0, \quad t \ge 0,$$ (4)

vorgeschrieben. Die Anfangsbedingungen sind

$$I(0,x)=0, \quad 0 < x \le a,$$ (5)

und

$$\begin{eqnarray*} R(0,x) = R_0\exp(-x/\mu),\quad S(0,x)=0, \quad 0 \le x \le a. \end{eqnarray*}$$

Die Anfangs- und Randbedingungen für Iod sind im Punkt $\;(t=0,x=0)\;$ in obiger Version inkompatibel. Eine Version mit kompatiblen Anfangs- und Randbedingungen erhält man, wenn man die Annahme macht, daß die Zudosierung des Iod am Rande zeitabhängig erfolgt. Ein (physikalisch sinnvoller) Dosierungsmechanismus ist durch

$$\begin{eqnarray*} I(t,0) = I_0(1- \exp(-\kappa t)) \end{eqnarray*}$$

gegeben.

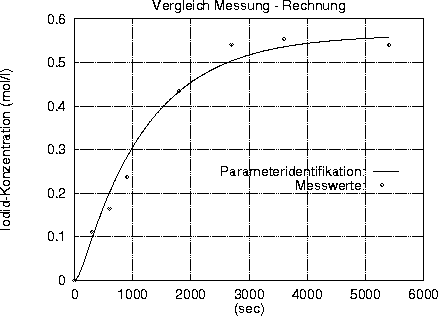
Wesentliche Größe für den Vergleich zwischen Messung und Rechnung ist der Zeitverlauf der (räumlich gemittelten) Iodid-Konzentration, gegeben durch

$$\begin{eqnarray*} h(t) = \frac{1}{\lambda}\int_0^b S(t,x)\exp(-x/\lambda)dx, \quad0 \le t \le T. \end{eqnarray*}$$

Dabei ist die Integration über eine bekannte Analysetiefe $\; 0 < b < a\;$ vorzunehmen, die durch die Meßtechnik vorgegeben ist.

Die Modellgleichungen lassen sich bei gegebenen Konstanten $\;D,c_1,c_2,I_0,R_0,\kappa,\lambda,\mu\;$ nach Standardmethoden numerisch lösen. Wesentlicher als dieses direkte Problem ist das inverse Problem: durch Vergleich Messung-Rechnung Aussagen über die beteiligten Konstanten zu gewinnen. Von besonderem Interesse sind die Reaktionskonstante $\;c_1\;$ und die Anfangskonzentration der Radikale $\;R_0\;$. Ein typisches Ergebnis einer derartigen Parameteridentifikation ist in der Abbildung gegeben.

Es ist unbekannt, ob eine eindeutige Bestimmung z. B. dieser Parameter durch die gegebene Meßgröße möglich ist. Zur Beurteilung der Ergebnisse ist eine enge Zusammenarbeit mit dem Kooperationspartner unerläßlich.