




Next: Forschungsgruppe Dynamische Systeme und Steuerungstheorie
Up: Projektbeschreibungen
Previous: Phasenfeldgleichungen und Stefan-Probleme
Bearbeiter: P. Krejcí
,
M. Siegfanz
,
J. Sprekels
Kooperation: M. Brokate (Christian-Albrechts-Universität zu Kiel),
D. Rachinskii (Institut für Probleme der Informationsübertragung, Moskau)
Beschreibung der Forschungsarbeit:
Ziel dieses Projektes ist es, realistische Modelle für die Evolution
von Systemen herzuleiten, in denen Nichtlinearitäten
vom Hysterese-Typ auftreten. Von besonderem Interesse für die
Anwendungen sind dabei Fragen der (Thermo-) Elastoplastizität und der
Phasenübergänge.
a) In [1] wurden Stetigkeitseigenschaften der konstitutiven
Operatoren des isothermen nichtlinearen
Chaboche-Verfestigungsmodelles betrachtet, wobei der
Spannungstensor 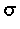 aus der plastischen
Komponente
aus der plastischen
Komponente 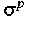 und der Verfestigungskomponente
und der Verfestigungskomponente 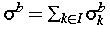 besteht, die mit der plastischen Dehnung
besteht, die mit der plastischen Dehnung
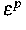 durch die Differentialgleichung
durch die Differentialgleichung
| 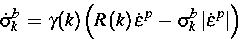 |
(1) |
mit Konstanten 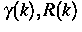 verbunden ist, und wobei
verbunden ist, und wobei
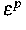 das von Misessche Kriterium erfüllt. Das
Materialgesetz wird implizit durch eine Differentialgleichung
ausgedrückt, die den mehrdimensionalen Spiel-Operator enthält. Neu
bewiesene Eigenschaften des Spiel-Operators ermöglichen den Nachweis,
daß totale Spannung und totale Dehnung stetig bezüglich der
gleichmäßigen Konvergenz im Raum der stetigen
Funktionen mit beschränkter Variation
voneienander abhängen.
das von Misessche Kriterium erfüllt. Das
Materialgesetz wird implizit durch eine Differentialgleichung
ausgedrückt, die den mehrdimensionalen Spiel-Operator enthält. Neu
bewiesene Eigenschaften des Spiel-Operators ermöglichen den Nachweis,
daß totale Spannung und totale Dehnung stetig bezüglich der
gleichmäßigen Konvergenz im Raum der stetigen
Funktionen mit beschränkter Variation
voneienander abhängen.
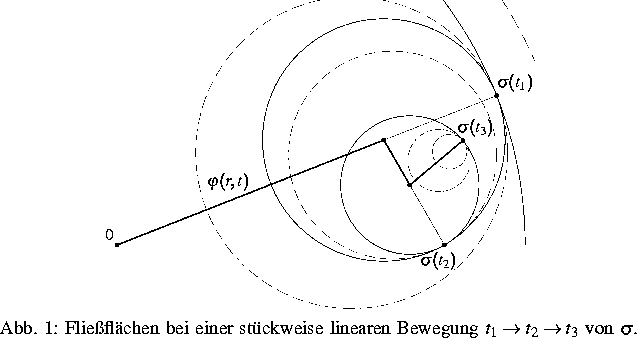
Das Mróz-Modell unterscheidet sich von anderen
Plastizitätsmodellen durch die Eigenschaft, daß individuelle
bewegliche Fließflächen mit verschiedenen Radien immer ineinander
eingeschlossen bleiben. Für den kontinuierlichen Mrózschen
Spannungs-Dehnungs-Operator, der Fließflächen aller Radien enthält
(siehe Abb. 1, wo 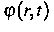 die Mittelpunktskurve bezeichnet),
wurden in [2] explizite Formeln für den inversen Operator zusammen mit
entsprechenden Energie-Ungleichungen abgeleitet. Ein Beispiel für die
Mehrdeutigkeit der Lösungen einer Anfangswertaufgabe für eine einfache
Differentialgleichung mit dem Mróz-Operator zeigt u. a., daß man keine
Lipschitz-Stetigkeit des Operators erwarten kann.
die Mittelpunktskurve bezeichnet),
wurden in [2] explizite Formeln für den inversen Operator zusammen mit
entsprechenden Energie-Ungleichungen abgeleitet. Ein Beispiel für die
Mehrdeutigkeit der Lösungen einer Anfangswertaufgabe für eine einfache
Differentialgleichung mit dem Mróz-Operator zeigt u. a., daß man keine
Lipschitz-Stetigkeit des Operators erwarten kann.
b) Wesentlich schwieriger als der isotherme Fall ist der Fall,
in dem die Temperatur als zusätzliche Zustandsvariable auftritt, da
nicht klar ist, wie dann freie Energie, innere Energie und
Entropie definiert und der Erste und Zweite Hauptsatz der
Thermodynamik angewendet werden können.
In [5] war es erstmalig gelungen, für temperaturabhängige PRANDTL-ISHLINSKII-Operatoren der Form
| ![\begin{displaymath}
\sigma\,=\,{\cal P} [\varepsilon]\,=\,\int_0^\infty \varphi (r, \theta)
{\frak s}_r [\varepsilon]\,d r\,,\end{displaymath}](../../1997/html/images/img124.gif) |
(2) |
(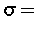 Spannung,
Spannung, 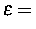 Verzerrung,
Verzerrung, 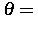 absolute Temperatur,
absolute Temperatur, 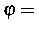 Dichtefunktion,
Dichtefunktion, 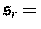 elastisch-plastisches Element zur Schwelle
elastisch-plastisches Element zur Schwelle 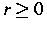 ) eine
thermodynamisch konsistente Theorie der Thermoplastoelastizität zu
entwickeln. Die grundlegende Idee beruht darauf, die in [3]
ausgeführte Theorie der Hysteresis-Potentiale zu
verallgemeinern. Freie Energie, innere Energie und Entropie ergeben
sich dann als Operatoren, nicht länger als Funktionen, und
man erhält eine Thermodynamik von Operatoren.
) eine
thermodynamisch konsistente Theorie der Thermoplastoelastizität zu
entwickeln. Die grundlegende Idee beruht darauf, die in [3]
ausgeführte Theorie der Hysteresis-Potentiale zu
verallgemeinern. Freie Energie, innere Energie und Entropie ergeben
sich dann als Operatoren, nicht länger als Funktionen, und
man erhält eine Thermodynamik von Operatoren.
Dieses Konzept wurde in der Arbeit [6] für eindimensionale
thermoelastoplastische Materialien mit Viskosität erfolgreich
umgesetzt. Man erhält dabei Zustandsgleichungen der Form (Massedichte
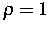 gesetzt)
gesetzt)
| 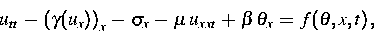 |
(3) |
| ![\begin{displaymath}
\left(C_V\,\theta\,+\,{\cal V}\, [u_x,
\theta]\right)_t\,-\...
...\mu\,u^2_{xt}\,-\,\beta\,\theta\,u_{xt}\,+\,g (\theta, x, t)\,,\end{displaymath}](../../1997/html/images/img133.gif) |
(4) |
mit Konstanten 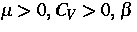 , wobei
, wobei 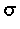 durch (2)
und
durch (2)
und 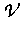 durch
durch
| ![\begin{displaymath}
{\cal V}\, [u_x, \theta]\,=\,\frac{1}{2} \int_0^\infty \left...
..._\theta \left(r,
\theta\right)\right)\,{\frak s}_r^2 [u_x]\,dr\end{displaymath}](../../1997/html/images/img136.gif) |
(5) |
gegeben sind. Es gelang in [6], Existenz und Eindeutigkeit einer
Lösung 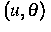 für eine Anfangsrandwertaufgabe für dieses
System zu zeigen. Die Asymptotik des Systems für
für eine Anfangsrandwertaufgabe für dieses
System zu zeigen. Die Asymptotik des Systems für 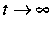 wurde in [10] untersucht.
wurde in [10] untersucht.
c) Hysteresephänomene sind häufig Begleiterscheinungen von
Phasenübergängen. Letztere werden gern durch
Phasenfeldgleichungen (z. B. Caginalp-Modell,
Penrose-Fife-Modell, siehe [3]) mathematisch modelliert, wobei die
Hysteresis als Konsequenz einer Nicht-Konvexität der freien Energie
gedeutet wird.
Im Berichtszeitraum wurde zu diesem Problemkomplex ein völlig neuer
Zugang entwickelt: Anstatt eine nichtkonvexe freie Energie anzunehmen,
wurde die Hysterese nunmehr in der Form von Hysterese-Operatoren
direkt in die Phasenfeldgleichungen aufgenommen. Man erhält dabei
Systeme der Form
| ![\begin{displaymath}
\mu\,w_t\,+\,{\cal H}_1 [w]\,+\,{\cal H}_2 [w]\,\theta\,=\,0\,,\end{displaymath}](../../1997/html/images/img139.gif) |
(6) |
| ![\begin{displaymath}
\left(C_V\,\theta\,+\,{\cal F}_1
[w]\right)_t\,-\,\kappa\,\Delta \theta\,=\,g (\theta, x, t)\,,\end{displaymath}](../../1997/html/images/img140.gif) |
(7) |
wobei 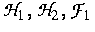 geeignete
Hysterese-Operatoren sind. Motiviert wurde dieser Zugang dadurch,
daß sich Modellierungen mit Hilfe von Variationsungleichungen, wie
z. B. das klassische relaxierte Stefan-Problem, auf die Form
(6), (7) transformieren lassen. Dabei sorgt die vorausgesetzte
Dissipativität der Hysterese-Operatoren
geeignete
Hysterese-Operatoren sind. Motiviert wurde dieser Zugang dadurch,
daß sich Modellierungen mit Hilfe von Variationsungleichungen, wie
z. B. das klassische relaxierte Stefan-Problem, auf die Form
(6), (7) transformieren lassen. Dabei sorgt die vorausgesetzte
Dissipativität der Hysterese-Operatoren 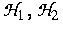 (vgl. auch [3]) dafür, daß der Zweite Hauptsatz der
Thermodynamik in Form der Entropieungleichung erfüllt ist.
(vgl. auch [3]) dafür, daß der Zweite Hauptsatz der
Thermodynamik in Form der Entropieungleichung erfüllt ist.
Es gelang im Berichtszeitraum in den Arbeiten [7, 9], die eindeutige
Lösbarkeit einer Anfangsrandwertaufgabe für das System (6), (7) zu
beweisen. Ein analoger Beweis gelang in [8] für das (6), (7)
entsprechende Modell vom Penrose-Fife-Typ.
Der im Berichtszeitraum entwickelte neue Ansatz zur Behandlung von
Phasenfeldsystemen ist sehr erfolgversprechend und soll im Jahre 1998
verstärkt untersucht werden.
Projektliteratur:
- M. BROKATE, P. KREJCí,
Maximum norm wellposedness of nonlinear kinematic hardening
models, Cont. Mech. Thermodyn., 9 (1997), pp. 365-380.
- M. BROKATE, P. KREJCí, D. RACHINSKII,
Some analytical properties of the multidimensional continuous
Mróz model of plasticity, WIAS-Preprint No. 391 (1998)
,
erscheint in: Control & Cybernetics.
- M. BROKATE, J. SPREKELS,
Hysteresis and Phase Transitions, Appl. Math. Sci.,
Vol. 121, Springer-Verlag, New York 1996.
- P. KREJCí,
Hysteresis, Convexity and Dissipation in Hyperbolic Equations,
Gakuto Int. Series, Vol. 8, Gakk
 tosho, Tokyo 1996.
tosho, Tokyo 1996.
- P. KREJCí, J. SPREKELS,
On a system of nonlinear PDEs with temperature-dependent
hysteresis in one-dimensional thermoplasticity,
J. Math. Anal. Appl., 209 (1997), pp. 25-46.
- P. KREJCí, J. SPREKELS,
Temperature-dependent hysteresis in one-dimensional
thermovisco-elastoplasticity,
WIAS-Preprint No. 344 (1997)
,
erscheint in: Appl. Math.
- P. KREJCí, J. SPREKELS,
A hysteresis approach to phase-field models,
WIAS-Preprint No. 364 (1997)
, erscheint in:
Nonlin. Anal. TMA.
- P. KREJCí, J. SPREKELS,
Hysteresis operators in phase-field models of Penrose-Fife
type, WIAS-Preprint No. 390 (1998)
,
erscheint in: Appl. Math.
- P. KREJCí, J. SPREKELS,
Hysteresis operators in phase-field models, erscheint in:
Progress in Nonlinear Partial Differential Equations and their
Applications, Birkhäuser Verlag, Basel 1998.
- P. KREJCí, J. SPREKELS,
Weak stabilization of solutions to PDEs with hysteresis in
thermovisco-elastoplasticity, erscheint in: Proceedings of EQUADIFF
9, 1997.





Next: Forschungsgruppe Dynamische Systeme und Steuerungstheorie
Up: Projektbeschreibungen
Previous: Phasenfeldgleichungen und Stefan-Probleme
LaTeX typesetting by I. Bremer
1/18/1999
![]() aus der plastischen
Komponente
aus der plastischen
Komponente ![]() und der Verfestigungskomponente
und der Verfestigungskomponente ![]() besteht, die mit der plastischen Dehnung
besteht, die mit der plastischen Dehnung
![]() durch die Differentialgleichung
durch die Differentialgleichung

![]() die Mittelpunktskurve bezeichnet),
wurden in [2] explizite Formeln für den inversen Operator zusammen mit
entsprechenden Energie-Ungleichungen abgeleitet. Ein Beispiel für die
Mehrdeutigkeit der Lösungen einer Anfangswertaufgabe für eine einfache
Differentialgleichung mit dem Mróz-Operator zeigt u. a., daß man keine
Lipschitz-Stetigkeit des Operators erwarten kann.
die Mittelpunktskurve bezeichnet),
wurden in [2] explizite Formeln für den inversen Operator zusammen mit
entsprechenden Energie-Ungleichungen abgeleitet. Ein Beispiel für die
Mehrdeutigkeit der Lösungen einer Anfangswertaufgabe für eine einfache
Differentialgleichung mit dem Mróz-Operator zeigt u. a., daß man keine
Lipschitz-Stetigkeit des Operators erwarten kann.
![]() gesetzt)
gesetzt)