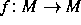 ein
ein
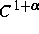 -Diffeomorphismus mit einem invarianten Maß
-Diffeomorphismus mit einem invarianten Maß
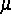 .
.





Bearbeiter: J. Schmeling
Kooperation: L. Barreira (Instituto Superior Técnico, Lissabon), Y. Pesin (Pennsylvania State University, Department of Mathematics, University Park), S. Troubetzkoy (University of Alabama at Birmingham, Department of Mathematics)
Förderung: Deutsche Akademie der Naturforscher Leopoldina
Beschreibung der Forschungsarbeit:
In diesem Projekt befassen wir uns mit dem lange Zeit offenen
grundlegenden Problem der Existenz der punktweisen Dimension
invarianter Maße. Dieses Problem wurde explizit von L.-S. Young auf
ihrer Rede auf dem Internationalen Mathematikerkongreß 1994 in Zürich hervorgehoben und ist als
Eckmann-Ruelle-Vermutung allgemein bekannt. Es kann auf folgende Weise
formuliert werden. Sei M eine kompakte glatte Riemannsche
Mannigfaltigkeit und 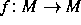 ein
ein
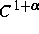 -Diffeomorphismus mit einem invarianten Maß
-Diffeomorphismus mit einem invarianten Maß
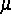 .
.
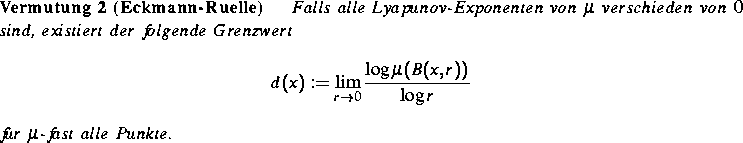
Der obere Grenzwert wird die punktweise Dimension von 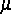 in
X genannt. Die Existenz des Grenzwertes impliziert den grundlegenden
Fakt, daß alle Dimensionscharakteristiken des Maßes
übereinstimmen. Dieser gemeinsame Wert ist eine fundamentale Größe der
fraktalen Struktur von
in
X genannt. Die Existenz des Grenzwertes impliziert den grundlegenden
Fakt, daß alle Dimensionscharakteristiken des Maßes
übereinstimmen. Dieser gemeinsame Wert ist eine fundamentale Größe der
fraktalen Struktur von 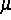 . Damit spielt die
Eckmann-Ruelle-Vermutung in der Dimensionstheorie eine
analoge Rolle zum Satz von Shannon-McMillan-Breiman in der
Entropietheorie.
. Damit spielt die
Eckmann-Ruelle-Vermutung in der Dimensionstheorie eine
analoge Rolle zum Satz von Shannon-McMillan-Breiman in der
Entropietheorie.
Da hyperbolische Maße beim Studium physikalischer Modelle chaotischer Systeme mit fraktaler Struktur eine wesentliche Rolle spielen, kann man die Eckmann-Ruelle-Vermutung auch als Basis derartiger Studien betrachten.
Die Eckmann-Ruelle-Vermutung ist insofern scharf, daß man keine der Voraussetzungen abschwächen kann und bezieht sich somit auf die breitestmögliche Klasse von Maßen.
In [1] ist es L. Barreira, Y. Pesin und mir gelungen, die Eckmann-Ruelle-Vermutung in voller Allgemeinheit zu beweisen. Außerdem konnten S. Troubetzkoy und ich ein analoges Resultat für Endomorphismen erzielen [2].
Projektliteratur:




