




Next: Probleme der Theorie
Up:
Previous: Geometrie von Basismengen
Bearbeiter: H. G. Bothe
Beschreibung der Forschungsarbeit:
In [1] konnte gezeigt werden, daß eindimensionale
hyperbolische Attraktoren 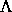 in mindestens vierdimensionalen
Mannigfaltigkeiten unter schwachen Voraussetzungen durch ihre innere
Struktur die Topologie ihres Einzugsbereiches bestimmen und daß sich
diese Einzugsbereiche als kartesisches Produkt einer offenen Teilmenge
in mindestens vierdimensionalen
Mannigfaltigkeiten unter schwachen Voraussetzungen durch ihre innere
Struktur die Topologie ihres Einzugsbereiches bestimmen und daß sich
diese Einzugsbereiche als kartesisches Produkt einer offenen Teilmenge
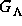 der dreidimensionalen Sphäre
der dreidimensionalen Sphäre 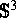 mit einem Raum
mit einem Raum 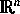 ergeben. Jetzt konnte in wichtigen Fällen aus der inneren Struktur von
ergeben. Jetzt konnte in wichtigen Fällen aus der inneren Struktur von
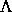 auf den topologischen Typ von
auf den topologischen Typ von 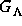 geschlossen
werden. Es ergab sich, daß
geschlossen
werden. Es ergab sich, daß 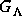 ein offener Henkelkörper, das
Komplement eines unendlich verknoteten Bündels aus endlich vielen
geschlossenen Kurven oder eine Mannigfaltigkeit sein kann, die in dem
Sinne ausgefranst ist, daß sie bei jeder topologischen Einbettung in
ein offener Henkelkörper, das
Komplement eines unendlich verknoteten Bündels aus endlich vielen
geschlossenen Kurven oder eine Mannigfaltigkeit sein kann, die in dem
Sinne ausgefranst ist, daß sie bei jeder topologischen Einbettung in
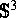 einen nicht lokal zusammenhängenden Rand haben muß.
einen nicht lokal zusammenhängenden Rand haben muß.
Projektliteratur:
- H. G. Bothe, How hyperbolic attractors determine
their basins, Nonlinearity, 9 (1996), pp. 173--190.
- H. G. Bothe, Topology of the basins of
hyperbolic attractors, WIAS-Preprint No. 311, Berlin 1997.
wwwadmin@wias-berlin.de
Mon Feb 17 13:38:21 MET 1997
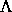 in mindestens vierdimensionalen
Mannigfaltigkeiten unter schwachen Voraussetzungen durch ihre innere
Struktur die Topologie ihres Einzugsbereiches bestimmen und daß sich
diese Einzugsbereiche als kartesisches Produkt einer offenen Teilmenge
in mindestens vierdimensionalen
Mannigfaltigkeiten unter schwachen Voraussetzungen durch ihre innere
Struktur die Topologie ihres Einzugsbereiches bestimmen und daß sich
diese Einzugsbereiche als kartesisches Produkt einer offenen Teilmenge
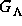 der dreidimensionalen Sphäre
der dreidimensionalen Sphäre 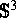 mit einem Raum
mit einem Raum 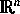 ergeben. Jetzt konnte in wichtigen Fällen aus der inneren Struktur von
ergeben. Jetzt konnte in wichtigen Fällen aus der inneren Struktur von
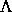 auf den topologischen Typ von
auf den topologischen Typ von 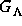 geschlossen
werden. Es ergab sich, daß
geschlossen
werden. Es ergab sich, daß 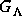 ein offener Henkelkörper, das
Komplement eines unendlich verknoteten Bündels aus endlich vielen
geschlossenen Kurven oder eine Mannigfaltigkeit sein kann, die in dem
Sinne ausgefranst ist, daß sie bei jeder topologischen Einbettung in
ein offener Henkelkörper, das
Komplement eines unendlich verknoteten Bündels aus endlich vielen
geschlossenen Kurven oder eine Mannigfaltigkeit sein kann, die in dem
Sinne ausgefranst ist, daß sie bei jeder topologischen Einbettung in
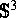 einen nicht lokal zusammenhängenden Rand haben muß.
einen nicht lokal zusammenhängenden Rand haben muß.




