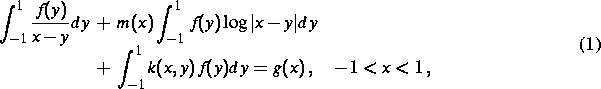Integralgleichungsmethoden in Elastizitätstheorie und Tragflügeltheorie

Bearbeiter: J. Elschner, S. Prößdorf, G. Schmidt  

Kooperation: V. Maz'ya, T. Ivanov (Universität Linköping), I. H. Sloan (The University of New South Wales, Sydney), Y. Jeon (Ajou University, Suwon), E. P. Stephan (Universität Hannover), S. Okada (The University of Tasmania, Hobart), G. Monegato, L. Scuderi (Politecnico di Torino)

Beschreibung der Forschungsarbeit:

Zu diesem Projekt wurden 1996 folgende Arbeiten durchgeführt:

1. Berechnung spezieller Integraloperatoren der ebenen Elastizitätstheorie und die Kubatur von Potentialen in beschränkten Gebieten

   Iterative Integralgleichungsmethoden sind ein interessantes alternatives Lösungsverfahren für nichtlineare Randwertaufgaben der Elastizitätstheorie, wenn es gelingt, effektive Approximationen für elastische und verwandte Potentiale zu entwickeln. Aufbauend auf den in vergangenen Jahren entwickelten und begründeten semi-analytischen Kubaturformeln für Integraloperatoren der mathematischen Physik, die numerisch effizient sind für glatte Funktionen mit kompaktem Träger (vgl. [4]), wurde die Anwendung von Wavelet-Techniken und der Fall beschränkter Integrationsgebiete untersucht. In [5] wurde eine approximative Multiresolution entwickelt, mit deren Hilfe Räume von glatten, schnell abfallenden Ansatzfunktionen in fast orthogonale Wavelet-Räume zerlegt werden können. Durch die fast verschwindenden Momente dieser Wavelets gelingt es, semi-analytische, schwach besetzte Matrix-Darstellungen wichtiger Integraloperatoren der mathematischen Physik anzugeben. In [3] wurde ein anderer Zugang für die Kubatur von Integraloperatoren in beschränkten Gebieten untersucht, der auf der Quasiinterpolation der Dichte auf speziellen, sich zum Rand hin häufenden Gitterpunkten basiert. Neben Abschätzungen des Approximationsfehlers wurde die optimale Wahl der Gitterverfeinerung beschrieben. Darüber hinaus wurden Computerprogramme zur Approximation von Funktionen in polygonalen Gebieten und zur Berechnung spezieller Integraloperatoren der ebenen Potential- und Elastizitätstheorie implementiert.

2. Lösung des Zaremba-Problems in Gebieten mit Ecken

   Mellinsche Faltungsgleichungen stellen eine wichtige Klasse nichtkompakter Integralgleichungen dar, die insbesondere in der Bruchmechanik (z. B. Berechnung der Spannungsverteilung bei 2D-Rißproblemen) und bei der Lösung vieler anderer Randwertaufgaben der mathematischen Physik und Mechanik in Gebieten mit nichtglatten Rändern auftreten. Bei der numerischen Lösung derartiger Integralgleichungen haben sich in letzter Zeit Approximationsverfahren mit trigonometrischen Ansatzfunktionen als sehr effektiv erwiesen. Insbesondere wurde ein optimal konvergentes Kollokationsverfahren für das Zaremba-Problem in Gebieten mit Ecken entwickelt und numerisch getestet [2], wobei Transformationstechniken zur Glättung der Lösungssingularitäten mit der FFT zur schnellen Lösung der entstehenden Gleichungssysteme gekoppelt wurden. Die theoretische Begründung (Stabilität) dieser Verfahren stellt für Integralgleichungen mit Mellinschen Faltungskernen ein schwieriges Problem dar, das zur Zeit noch nicht zufriedenstellend gelöst ist. In [1] gelang es erstmalig, explizite hinreichende und notwendige Bedingungen für die Stabilität des Galerkinverfahrens mit trigonometrischen Polynomen aufzustellen, wobei auch der Fall eines Systems solcher Gleichungen erfaßt wurde.

3. Analytische und numerische Lösung der Tragflügelgleichung mit logarithmischem Zusatzkern

   Bei der Berechnung der Zirkulation beim freifahrenden schwach belasteten Propeller und bei der Lösung der Fundamentalprobleme der ebenen Elastizitätstheorie treten singuläre Integralgleichungen der Gestalt

    

   auf. In [7] wurden die Lösbarkeitsverhältnisse (einschließlich des Singulärverhaltens der Lösungen) in den gewichteten Räumen mit 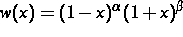, , 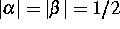vollständig geklärt. Im Falle der ungestörten Gleichung 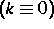und 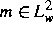wurden alle Lösungen explizit angegeben. Mit Hilfe dieser Lösungen wurde eine zu (1) äquivalente Fredholmsche Integralgleichung hergeleitet. In Form einer Normabschätzung für k ließ sich eine einfache hinreichende Bedingung dafür angegeben, daß (1) für jede rechte Seite g genau eine einparametrige Lösungsschar in einem geeigneten Hilbertraum 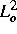besitzt. Damit wurden bekannte Ergebnisse von Müller [6] und Schleiff [8] wesentlich verallgemeinert. Unter Benutzung der Lösbarkeitstheorie wurde ein numerisches Verfahren mit orthogonalen Polynomen als Ansatzfunktionen beschrieben, für das Stabilität und optimale Fehlerabschätzungen in einer Skala von gewichteten Sobolev-Normen und gleichmäßigen Normen bewiesen wurden [7].

   Im Falle unstetiger rechter Seiten g (Flügelschlag) wurde eine in der Forschungsgruppe entwickelte Transformationstechnik zur Glättung der Lösungssingularitäten in den Sprungstellen von g mit einem trigonometrischen Kollokationsverfahren gekoppelt. Durchgeführte numerische Tests bestätigen die hohe Effizienz dieser Methode. Die Stabilitäts- und Konvergenzuntersuchungen werden in Zusammenarbeit mit G. Monegato und L. Scuderi (Politecnico di Torino) fortgesetzt.

Projektliteratur:

1.   J. ELSCHNER, Trigonometric approximation of Mellin convolution equations, wird eingereicht in: J. Integral Equations Appl.

2.   J. ELSCHNER, Y. JEON, I. H. SLOAN, E. P. STEPHAN, The collocation method for mixed boundary value problems on domains with curved polygonal boundaries, erscheint in: Numer. Math.

3.   T. IVANOV, V. MAZ'YA, G. SCHMIDT, Boundary layer approximations and cubature of potentials in domains, in Vorbereitung.

4.   V. MAZ'YA, G. SCHMIDT, ``Approximate Approximations'' and the cubature of potentials, Rend. Mat. Acc. Lincei, Serie 9, Vol. 6 (1995), pp. 161--184.

5.   V. MAZ'YA, G. SCHMIDT, Approximate wavelets and the approximation of pseudodifferential operators, WIAS-Preprint No. 249, Berlin 1996.

6.   H. N. MÜLLER, Über eine singuläre Integralgleichung 1. Art mit Zusatzkern, Math. Nachr., 35 (1967), pp. 57--74.

7.   S. OKADA, S. PRÖSSDORF, On the solution of the generalized airfoil equation, WIAS-Preprint No. 242, Berlin 1996; erscheint in: J. Integral Equations Appl.

8.   M. SCHLEIFF, Über eine singuläre Integralgleichung mit logarithmischem Zusatzkern, Math. Nachr., 42 (1969), pp. 79--88.