Analytische und numerische Behandlung direkter und inverser Probleme für diffraktive Strukturen in der Optik

Bearbeiter: J. Elschner, G. Schmidt  

Kooperation: B. Kleemann, H.-J. Rostalski (Berliner Institut für Optik GmbH, (BIFO))

Beschreibung der Forschungsarbeit:

Die Entwicklung verschiedener hochpräziser Mikro-Techniken erlaubt heute die Herstellung mikrooptischer Elemente mit komplexen Oberflächenprofilen und Strukturgrößen, die im Bereich der Wellenlänge des Lichts liegen. Da bei Strukturen kleiner als fünf mal der Wellenlänge Polarisations- und Resonanzeffekte auftreten, ergeben sich durch die Mikrostrukturierung von Ober- und Grenzflächen qualitativ neue Anwendungsmöglichkeiten der Optik, deren Nutzung in verschiedenen Bereichen der Verfahrens-, Umwelt- und Medizintechnik enorme Potentiale bietet. Für die Bestimmung der Wirkung eines optischen Gitters oder für die optimale Anpassung der beugenden Struktur gewinnt die numerische Simulation immer größere Bedeutung. Allerdings reichen die bisher benutzten Ansätze der skalaren Beugungstheorie für Modellierung und Berechnung solcher Strukturen nicht mehr aus. Gegenstand der Arbeiten, die im Rahmen einer Forschungsvereinbarung mit dem BIFO durchgeführt werden, ist die Untersuchung exakterer Modelle (auf der Basis von Transmissionsproblemen für die elektromagnetischen Feldgleichungen) und deren analytische und numerische Behandlung. Die Hauptanwendung liegt in der Entwicklung effektiver numerischer Methoden zur Lösung von Optimal-Design-Problemen für binäre Gitter, die am BIFO entworfen werden. Von Interesse ist dabei u. a. die Wirkungsgraderhöhung von Solarmodulen, von Mikrooptiken in Hochleistungslasern, von HR-Spiegeln und Polarisationsschaltern.

1996 wurden zu dieser Thematik folgende Arbeiten durchgeführt:

1. Entwicklung und Implementierung effektiver Algorithmen zur Lösung des direkten Problems bei binären periodischen Gittern:

   Hierbei wird die Invarianz des Problems bezüglich einer Raumdimension und der Fall einer ebenen einfallenden Welle angenommen. Das elektromagnetische Feld läßt sich aus den Transversalkomponenten des elektrischen (TE) und des magnetischen Feldes (TM) bestimmen, die im 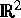Transmissionsprobleme für die Helmholtz-Gleichungen

    

   mit stückweise stetigen Diffraktionskoeffizienten k und bekannten Ausstrahlungsbedingungen erfüllen. Da das Gitterprofil eine periodische Funktion ist, können die Lösungen u als quasiperiodische Funktionen gesucht werden, die (1) in einem Rechteck erfüllen und nichtlokalen Randbedingungen genügen, die durch hypersinguläre Integraloperatoren erzeugt werden. Außerdem müssen gewisse Transmissionsprobleme an den Materialgrenzen (Interface) erfüllt sein. Die Realisierung der Ausstrahlungsbedingungen in Form nichtlokaler Randbedingungen und die Variationsformulierung der entsprechenden Randwertaufgaben geht auf Untersuchungen von Bao/Dobson/Friedman (vgl. [1], [5]) zurück, die damit Existenz- und Eindeutigkeitsaussagen für die direkten Probleme beweisen konnten. Eine FE/BE-Diskretisierung der Variationsgleichungen bietet sich als numerisches Lösungsverfahren an. Zur Lösung der direkten Probleme bei binären Gittern und stückweise konstantem k wurde ein auf bilinearen Ansatzfunktionen basierendes Verfahren implementiert. Das entstehende Gleichungssystem besitzt eine tridiagonale Struktur mit teilweise vollbesetzten Blöcken und ist nicht symmetrisch. Deshalb wird zur Lösung die Matrix-Progonka genutzt, die wegen der Geometrie der Beugungsgitter mit der FFT gekoppelt werden kann. Zahlreiche numerische Tests und Vergleiche mit der Integralgleichungsmethode haben gezeigt, daß diese Methode bei einer Vielzahl der heute die Anwender interessierenden Beugungsgitter recht genaue Resultate für die Kenngrößen der Beugungsgitter, die sogenannten Beugungs- und Transmissionseffektivitäten, liefert. Allerdings entstehen insbesondere bei großem k und großen Schichtdicken die bei Gebietsverfahren für die Wellengleichung charakteristischen Dispersionseffekte, die eine sehr feine Diskretisierung erfordern. Um die direkten Probleme auch für diese Beispiele in vertretbarem Zeitaufwand lösen zu können, wurde der oben genannte Zugang weiterentwickelt, u. a. als verallgemeinerte FEM (nach Babuska) mit minimaler Pollution, mathematisch begründet und implementiert (vgl. [4]). Dadurch konnte die Effektivität des Verfahrens erheblich erhöht werden.

   

2. Das die Ingenieure eigentlich interessierende Problem des Entwurfs diffraktiver Strukturen, die bestimmte optische Eigenschaften oder Funktionen realisieren, ist ein optimales Design-Problem. Zu seiner Lösung müssen neuere Methoden (vgl. [2], [3], [6]) zur Lösung von Identifizierungs- und Optimierungsproblemen für Randwertaufgaben genutzt und weiterentwickelt werden, deren theoretische Begründung bei Transmissionsproblemen mit nichtglattem Interface offen ist.

   Die Bestimmung optimaler binärer Gitter führt oft auf Minimumprobleme für Zielfunktionen, die von Beugungs- und Transmissionskoeffizienten bzw. -effektivitäten für den TE- und TM-Fall abhängen. Für eine große Klasse dieser Funktionen wurde die Differenzierbarkeit bezüglich Variationen des binären Gitterprofils bewiesen, und es wurden erstmalig effektive Berechnungsformeln für die Gradienten angegeben. Um diese Formeln mathematisch begründen zu können, ist es notwendig, die Singularitäten der Lösung von Transmissionsproblemen für die Helmholtz-Gleichung mit komplexem k in den Interface-Ecken zu untersuchen (vgl. [4]).

   Die oben genannte Variationsformulierung des Beugungsproblems hat den Vorteil, daß die zur Gradientenberechnung benötigten direkten und dualen Probleme parallel gelöst werden können. Auf der Grundlage der verallgemeinerten FEM wurden verschiedene Gradientenverfahren zur Minimabestimmung der Zielfunktionen implementiert und numerisch getestet. Da die Zielfunktionen in der Regel mehrere lokale Minima besitzen, wurden verschiedene Verfahren zur Ermittlung geeigneter Startwerte getestet. Mit dem entwickelten Programmsystem ist es z. Zt. möglich, binäre Gitter zu bestimmen, die über einem Bereich von Wellenlängen oder Einfallswinkeln vorgegebene Intensitäten optimieren bzw. Phasendifferenzen zwischen den TE- und TM-Polarisationen realisieren.

   Durch die Vielzahl der Anwendungsmöglichkeiten optischer Gitter und der damit zusammenhängenden optimalen Design-Probleme ist es notwendig, weitere Zielfunktionen und entsprechende Optimierungsalgorithmen zu untersuchen.

Projektliteratur:

1.   G. BAO, D. DOBSON, J. COX, Mathematical studies in rigorous grating theory, J. Opt. Soc. Am., A 10 (1995), pp. 1029--1042.
2.   D. COLTON, R. KRESS, Inverse acoustic and electromagnetic scattering theory, Springer, Berlin 1992.
3.   D. DOBSON, Optimal design of periodic antireflexive structures for the Helmholtz equation, Eur. J. Appl. Math., 4 (1993), pp. 321--340.
4.   J. ELSCHNER, G. SCHMIDT, Optimal design of binary diffractive gratings -- analysis and numerics, WIAS-Preprint, in Vorbereitung.
5.   A. FRIEDMAN, Mathematics in industrial problems, Part 7, Chap. 14, Vol. 67 of the IMA Vol. Math. Appl., Springer, New York, 1995.
6.   J. Sokoowski, J. ZOLESIO, Introduction to shape optimization, Shape Sensitivity Analysis, Springer Series in Comp. Math., Vol. 16, New York, 1992.