




Bearbeiter: D. Peterhof, B. Sandstede
Kooperation: A. Scheel (Institut für Mathematik I, FU Berlin)
Förderung: Feodor-Lynen Stipendium der Alexander von Humboldt-Stiftung
Beschreibung der Forschungsarbeit:
Die Gleichung
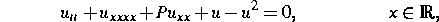
beschreibt Beulzustände von unendlich ausgedehnten Stäben, die auf einem abstoßenden elastischen Untergrund aufliegen. Die aufgetragene axiale Last ist dabei durch den Parameter P gegeben. In dieser Gleichung wurden von [Buffoni, Champneys, Toland] ein primärer und unendlich viele sekundäre lokalisierte Beulzustände mit endlicher Energie gefunden. Die sekundären Zustände bestehen aus mehreren, weit voneinander entfernten Kopien des primären Zustands. In [2] wurde die Stabilität dieser Beulzustände untersucht. Das Ergebnis hängt von der Belastungsart ab. Wird eine konstante Last aufgetragen (dead loading), so ist der primäre Beulzustand instabil. Falls dagegen die Verschiebung vorgegeben wird (rigid loading), so wird der primäre Zustand für kleine resultierende Lasten stabilisiert. Realistischer sind Modelle, die auf unendlichen Zylindern definiert sind und den Querschnitt berücksichtigen. Beulzustände lösen dann eine elliptische Differentialgleichung der Form
Mitte der achziger Jahre wurden Algorithmen zur numerischen Berechnung von lokalisierten Gleichgewichten dieser Gleichungen entwickelt. Bisher gibt es aber weder Konvergenz- noch Stabilitätsbeweise. Ebenso ist nicht bekannt, wie man Verzweigungen von sekundären Beulzuständen analysieren kann. In [1] haben wir begonnen, diese Probleme zu lösen. Die grundlegende Schwierigkeit ist, daß (1) schlecht gestellt ist! Wir konnten beweisen, daß der Funktionenraum so in zwei Komponenten zerlegt werden kann, daß die in einem primären Zustand linearisierten Gleichungen vorwärts bzw. rückwärts in der ersten bzw. zweiten Komponente gelöst werden können. Wir hoffen, damit in weiteren Arbeiten Verzweigungen von sekundären Zuständen behandeln sowie Fehlerabschätzungen für numerische Algorithmen geben zu können.
Projektliteratur:




