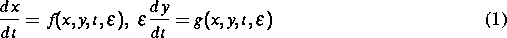
Bearbeiter: K. R. Schneider
Kooperation: Karmeshu (Jawaharlal Nehru University, New Delhi, Indien), N. N. Nefedov (Staatliche Universität Moskau, Rußland), A. Schuppert (Hoechst AG, Frankfurt/M.)
Beschreibung der Forschungsarbeit:
Die mathematische Modellierung zahlreicher Prozesse in der Biochemie und in anderen Gebieten der Naturwissenschaften führt auf Differentialgleichungssysteme mit mehreren Zeitskalen. Wir beschränken uns auf singulär gestörte Systeme der Gestalt
mit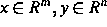 
.
Häufig ist die Dimension der schnellen Variablen y sehr groß (n
>>1), so daß nach einer adäquaten
Dimensionsreduktion gesucht wird, um qualitative Untersuchungen bzw.
online-fähige Berechnungen durchführen zu können. Unter bestimmten
Voraussetzungen
ist die Quasistationaritätsannahme dafür ein probates Mittel. In den
Fällen, wo diese Annahme nicht gerechtfertigt werden kann, liegt
entweder ein Schnitt von Gleichgewichtmannigfaltigkeiten des zu
(1)
gehörenden assoziierten Systems
vor, was mit einer Änderung des Stabilitätsverhaltens dieser Mannigfaltigkeiten verbunden ist, oder die Jacobi-Matrix von (1) wird in Unterräumen singulär. Im Berichtszeitraum wurde der Fall der Stabilitätsänderung weiter untersucht. Das grundlegende Problem besteht darin, ob eine Lösung sofort der neuen stabilen Mannigfaltigkeit folgt oder sich erst für einige Zeit nahe der alten, aber nunmehr instabil gewordenen Mannigfaltigkeit aufhält und dann in Richtung der stabilen Mannigfaltigkeit springt. Unter Verwendung der Technik der Ober- und Unterlösungen konnten neue Bedingungen für einen unmittelbaren Stabilitätswechsel abgeleitet werden. Für den Fall des verzögerten Stabilitätswechsels konnte mit derselben Technik bei skalaren nichtautonomen singulär gestörten Differentialgleichungen die asymptotische Verzögerungszeit bestimmt werden. Die Resultate über einen verzögerten Stabilitätsaustausch können mit zeitabhängigen Modellreduktionen bei singulär gestörten Systemen in Zusammenhang gebracht werden. Sie wurden ebenfalls zur Erklärung von verzögerten Sprüngen der Populationsdichte (unter Einschluß des Allee-Effektes) in der modifizierten logistischen Wachstumsgleichung verwendet. Weiterhin besteht ein Zusammenhang zu verzögerten Bifurkationen bei Systemen mit einem langsam veränderlichen Bifurkationsparameter. Diese Beziehung wurde genutzt, um eine neue Klasse von Relaxationsschwingungen zu begründen. Die Untersuchungen zu diesem Problemkreis sollen im Blick auf höherdimensionale Systeme fortgesetzt werden.
Projektliteratur:
