Bearbeiter: R. J. Rumpel, K. R. Schneider
Kooperation: L. M. Fridman (Samara Architecture and Building Academy, Rußland), F. Altpeter (École Polytechnique Fédérale de Lausanne, Schweiz), B. Michaeli (Universität Köln)
Beschreibung der Forschungsarbeit:
Viele dynamische Prozesse lassen sich als Systeme gewöhnlicher Differentialgleichungen mit Unstetigkeitsflächen modellieren. Die Unstetigkeiten können z. B. von der Steuerung (Relais) oder von mechanischen Kräften (trockene Reibung) herrühren. In solchen Systemen kann es zu Gleitbewegungen kommen, d. h. einem zeitweisen Verlauf der Trajektorie längs der Unstetigkeitsfläche. Diese Gleitzustände können mit der Methode der äquivalenten Steuerung von V. I. Utkin geeignet modelliert werden. Das Ziel der Untersuchungen bestand in der Übertragung von analytischen Methoden für glatte dynamische Systeme auf Systeme mit Gleitzuständen [4], wobei die bisher wenig untersuchten singulär gestörten Systeme mit Gleitzuständen (SGG-Systeme) im Mittelpunkt standen:
In [2] liegen Ergebnisse zur asymptotischen Entwicklung der Trajektorien des nichtdegenerierten Systems (1) vor, die auf der Randschichtmethode von A. B. Vasileva basieren. Die Dimension des Systems (1) läßt sich auf zwei verschiedene Möglichkeiten reduzieren:
a) durch Übergang zum reduzierten System (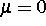
),
b) durch Beschränkung auf die Dynamik im Gleitgebiet
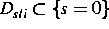(äquivalente Steuerung).
Die reduzierten Systeme wurden benutzt, um für SGG-System (1) Kriterien für Existenz, Stabilität und Persistenz periodischer Orbits herzuleiten. Sie beruhen auf Eigenschaften der Trajektorien an den Übergangsstellen zum und vom Gleitzustand, an denen die Lösungen nicht glatt sind. Zentrales Hilfsmittel ist die Einführung geeigneter Punktabbildungen vom Poincaréschen Typ auf dem Rand des Gleitgebiets.
Die Ergebnisse wurden auf ein SGG-System angewendet, das ein
Doppelpendel mit linearer Kopplung beschreibt, bei dem das Pendel
mit Masse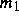 
auf einer gleichmäßig rotierenden Drehscheibe
mit Neigungswinkel 
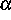aufliegt. Die Masse 
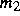des
anderen Pendels spielt die Rolle des kleinen Parameters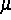 
.
Dieses SGG-System läßt sich mit kleinen Modifikationen als Roboterarm mit Störmasse interpretieren. Es erfüllt die Voraussetzungen der gefundenen Theoreme. Die Persistenz des stabilen periodischen Orbits ist in der Abbildung dokumentiert.
In der letzten Zeit wurde die Anwendbarkeit dieser Untersuchungen auf mechatronische SGG-Systeme mit mehreren Freiheitsgraden, insbesondere CNC-Maschinen [1], geprüft. Von technischer Relevanz ist die Betrachtung von Verbindungswellen, die in der Realität nie ganz starr sind. Als kleiner Parameter fungiert der Kehrwert der Steifigkeit. Es wurde nicht nur das klassische statische Reibmodell, sondern auch ein neuartiges dynamisches Reibmodell (Canudas de Wit et al.,1995) berücksichtigt. Dieses umfaßt sowohl die Geschwindigkeitsabhängigkeit (Stribeck-Effekt) als auch die Auslenkungsabhängigkeit (Dahl-Effekt / Auslenkungshysterese) der Reibung. Es wurden Simulationen zum Vergleich von dynamischem und statischem Reibmodell durchgeführt, die bestätigen, daß das statische Modell als Grenzfall des dynamischen Modells betrachtet werden kann.
Projektliteratur:
