




Next: Singulär gestörte Systeme
Up:
Previous: Optimale Steuerung diskontinuierlicher
Bearbeiter: F. Guyard,
R. Lauterbach,
D. Peterhof,
B. Sandstede
Kooperation: P. Chossat (INLN, Nizza),
B. Fiedler, A. Scheel, C. Wulff (FU Berlin)
Förderung: DFG-Schwerpunktprogramm ,,Strukturbildung in dissipativen
Systemen: Experiment und Theorie im quantitativen Vergleich``
DFG-Schwerpunktprogramm ,,Dynamik: Analysis, effiziente Simulation und
Ergodentheorie``
Feodor-Lynen Stipendium der Alexander von Humboldt-Stiftung
DAAD: Procope
Beschreibung der Forschungsarbeit:
Fragestellungen in Meteorologie, Geophysik und in vielen anderen Bereichen
führen auf hydrodynamische Probleme. Aus der Sicht der Theorie
dynamischer Systeme lassen sich diese erfolgreich behandeln,
wenn eine Reduktion auf einfachere Gleichungen die wesentlichen
Informationen über das Systemverhalten erhält. Die erzielten
Ergebnisse sind dann auf große Klassen von Problemstellungen
anzuwenden.
Für diese Form der Untersuchungen
spielen spezielle Strukturen in der Gleichung oft eine wichtige Rolle,
nicht zuletzt stellen Symmetrieüberlegungen oft eine ganze Bandbreite
mathematischer Methoden zur Verfügung.
1.) Polumkehr
Aus der Magnetisierung von Gesteinsproben kann man schließen, daß
das Erdmagnetfeld in Zeitskalen von 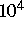 Jahren seine Orientierung
ändert. Nach einer langen Zeit stabiler Orientierung gibt es eine
vergleichsweise kurze Phase mit sehr komplizierten
Strukturen, auf die dann wieder eine lange Phase konstanter
Orientierung folgt,
allerdings mit vertauschten Polen.
Ein Zugang erklärt den sogenannten Geodynamo mit einer
Konvektionsbewegung geladener Flüssigkeiten in einer Schicht des
Erdkernes. Eine mathematische Beschreibung erfolgt mit den
Magnetohydrodynamischen Gleichungen. Ein mathematisches Objekt, das
qualitativ in der Lage ist, die obengenannten Orientierungswechsel
des Erdmagnetfeldes zu beschreiben, sind sogenannte heterokline Zyklen,
deren Existenz (oft) zur Folge hat, daß es Anfangswerte gibt, für die
die Lösung wieder in eine Umgebung des Ausgangspunktes zurückkehrt.
Solche sogenannten rekurrenten Strukturen sind typisch für das
Auftreten komplizierten dynamischen Verhaltens. Daraus ergibt sich die
natürliche Frage, ob es in dem System, das die Bewegung der
Flüssigkeit modelliert, solche heteroklinen Zykel gibt. In diesem Fall
führen die genannten Reduktionen auf gewöhnliche
Differentialgleichungen in Darstellungsräumen der Gruppe O(3). Für
solche Gleichungen ist bekannt, daß zumindest in der Nähe der
Instabilität der reinen Wärmeleitungslösung für Räume mit
irreduziblen Darstellungen keine heteroklinen Zykel existieren [6].
Solche Räume mit irreduziblen Darstellungen wären aber die natürlichen Räume für diese
Untersuchungen. Jedoch führen die Parameterwerte, die man
für das Beispiel der Erde für gegeben ansieht, auf eine
Darstellung einer Interaktion der
Jahren seine Orientierung
ändert. Nach einer langen Zeit stabiler Orientierung gibt es eine
vergleichsweise kurze Phase mit sehr komplizierten
Strukturen, auf die dann wieder eine lange Phase konstanter
Orientierung folgt,
allerdings mit vertauschten Polen.
Ein Zugang erklärt den sogenannten Geodynamo mit einer
Konvektionsbewegung geladener Flüssigkeiten in einer Schicht des
Erdkernes. Eine mathematische Beschreibung erfolgt mit den
Magnetohydrodynamischen Gleichungen. Ein mathematisches Objekt, das
qualitativ in der Lage ist, die obengenannten Orientierungswechsel
des Erdmagnetfeldes zu beschreiben, sind sogenannte heterokline Zyklen,
deren Existenz (oft) zur Folge hat, daß es Anfangswerte gibt, für die
die Lösung wieder in eine Umgebung des Ausgangspunktes zurückkehrt.
Solche sogenannten rekurrenten Strukturen sind typisch für das
Auftreten komplizierten dynamischen Verhaltens. Daraus ergibt sich die
natürliche Frage, ob es in dem System, das die Bewegung der
Flüssigkeit modelliert, solche heteroklinen Zykel gibt. In diesem Fall
führen die genannten Reduktionen auf gewöhnliche
Differentialgleichungen in Darstellungsräumen der Gruppe O(3). Für
solche Gleichungen ist bekannt, daß zumindest in der Nähe der
Instabilität der reinen Wärmeleitungslösung für Räume mit
irreduziblen Darstellungen keine heteroklinen Zykel existieren [6].
Solche Räume mit irreduziblen Darstellungen wären aber die natürlichen Räume für diese
Untersuchungen. Jedoch führen die Parameterwerte, die man
für das Beispiel der Erde für gegeben ansieht, auf eine
Darstellung einer Interaktion der 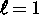 und
und 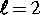 -Moden
(Kugelflächenfunktionen erster und zweiter Ordnung). Im nichtrotierenden Fall
haben Chossat und Armbruster [4] die Existenz heterokliner
Zykel in dieser Darstellung für gewisse Parameterwerte
nachgewiesen. Dieser Zykel ist allerdings nicht stabil
gegenüber Störungen, die die Symmetrie des Problems brechen (Rotation).
Methoden zur Untersuchung solcher Probleme mit erzwungener
Symmetriebrechung
gehen auf
[9] zurück. Die dort begonnenen Arbeiten wurden
innermathematisch
in [7, 8] ausgebaut. Diese Klassifizierung
zeigt, daß der aus [9] bekannte Weg, heterokline Zykel im
Fall gebrochener Symmetrien zu konstruieren, für eine Erklärung des
Verhaltens des Erdmagnetfeldes nicht geeignet ist.
Ideen, die eine Fortentwicklung der Arbeiten von Chossat und
Armbruster und von Lauterbach und Roberts sind, erlauben (unter vereinfachenden Annahmen)
in der
-Moden
(Kugelflächenfunktionen erster und zweiter Ordnung). Im nichtrotierenden Fall
haben Chossat und Armbruster [4] die Existenz heterokliner
Zykel in dieser Darstellung für gewisse Parameterwerte
nachgewiesen. Dieser Zykel ist allerdings nicht stabil
gegenüber Störungen, die die Symmetrie des Problems brechen (Rotation).
Methoden zur Untersuchung solcher Probleme mit erzwungener
Symmetriebrechung
gehen auf
[9] zurück. Die dort begonnenen Arbeiten wurden
innermathematisch
in [7, 8] ausgebaut. Diese Klassifizierung
zeigt, daß der aus [9] bekannte Weg, heterokline Zykel im
Fall gebrochener Symmetrien zu konstruieren, für eine Erklärung des
Verhaltens des Erdmagnetfeldes nicht geeignet ist.
Ideen, die eine Fortentwicklung der Arbeiten von Chossat und
Armbruster und von Lauterbach und Roberts sind, erlauben (unter vereinfachenden Annahmen)
in der 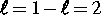 -Modeninteraktion
mit Rotation die Existenz stabiler heterokliner Zykel zu zeigen
[5].
-Modeninteraktion
mit Rotation die Existenz stabiler heterokliner Zykel zu zeigen
[5].
 Physikalisch bedeutungsvoll wären solche Zykel vor allem dann, wenn die
im Zyklus enthaltenen (relativen) Ruhelagen rein einmodig (
Physikalisch bedeutungsvoll wären solche Zykel vor allem dann, wenn die
im Zyklus enthaltenen (relativen) Ruhelagen rein einmodig (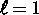 )
wären. In unseren bisherigen Untersuchungen konnten wir heterokline Zykel
und deren Stabilität nur nachweisen, wenn einmodige
)
wären. In unseren bisherigen Untersuchungen konnten wir heterokline Zykel
und deren Stabilität nur nachweisen, wenn einmodige 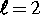 -
Gleichgewichtslagen auftreten. Unsere Untersuchungen deuten auf die
Existenz von Zyklen mit
einmodigen
-
Gleichgewichtslagen auftreten. Unsere Untersuchungen deuten auf die
Existenz von Zyklen mit
einmodigen 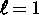 Gleichgewichten hin. Allerdings konnten dafür noch nicht
alle Beweisschritte durchgeführt
werden. Die Probleme liegen in der hohen Dimension des Parameterraumes
und der damit verbundenen Degeneriertheit des relevanten
Verzweigungsproblems. Wir vermuten jedoch, daß diese Zykel in der Nähe der
von uns beschriebenen Zykel gefunden werden können.
Gleichgewichten hin. Allerdings konnten dafür noch nicht
alle Beweisschritte durchgeführt
werden. Die Probleme liegen in der hohen Dimension des Parameterraumes
und der damit verbundenen Degeneriertheit des relevanten
Verzweigungsproblems. Wir vermuten jedoch, daß diese Zykel in der Nähe der
von uns beschriebenen Zykel gefunden werden können.
2.) Sphärisches Bénardproblem
In den bisher genannten Untersuchungen spielten Betrachtungen eines
Strömungsfeldes in einer Kugelschale eine große Rolle. Im Fall der
Polumkehr interessieren wir uns allerdings für ein Radienverhältnis
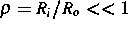 . Die Fälle
. Die Fälle 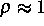 sind für Klimamodelle und
atmosphärische Vorgänge bedeutungsvoll. Allerdings kann man dieses
Problem nicht auf eine endlichdimensionale Dynamik reduzieren
[10]. Vielmehr muß man im Limes
sind für Klimamodelle und
atmosphärische Vorgänge bedeutungsvoll. Allerdings kann man dieses
Problem nicht auf eine endlichdimensionale Dynamik reduzieren
[10]. Vielmehr muß man im Limes 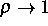 partielle
Differentialgleichungen als Grenzgleichungen betrachten. Für den Fall der
reinen Navier-Stokes Gleichungen wird die Dynamik für große
Anfangsbedingungen und Anregungen näherungsweise durch die
Navier-Stokes Gleichung auf der Kugeloberfläche beschrieben.
partielle
Differentialgleichungen als Grenzgleichungen betrachten. Für den Fall der
reinen Navier-Stokes Gleichungen wird die Dynamik für große
Anfangsbedingungen und Anregungen näherungsweise durch die
Navier-Stokes Gleichung auf der Kugeloberfläche beschrieben.
3.) Dynamik von Spiralwellen
Spiralwellen treten in den verschiedensten chemischen und
physikalischen Systemen auf. Experimentell sind diese raum-zeitlichen
Muster unter anderem in der Belousov-Zhabotinsky Reaktion, bei der
Katalyse an Platinoberflächen und in der Rayleigh-Bénard Konvektion
beobachtet worden. Sowohl in den Experimenten wie auch in numerischen
Simulationen findet man spontane Verzweigungen von starr-rotierenden
zu mäandernden Spiralwellen. Im Resonanzfall verzweigen driftende
Wellen. Mathematisch werden derartige Systeme durch
Reaktions-Diffusionssysteme
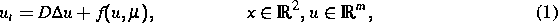
in der Ebene modelliert. Der Vektor u ist dann typischerweise durch
die Konzentrationen der chemischen Spezies gegeben. Gleichung
(1) ist äquivariant unter der euklidischen Gruppe
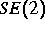 der Translationen und Rotationen. In [2] und
[3] haben wir die Dynamik in der Nähe von
Verzweigungspunkten auf endlich-dimensionale Zentrumsmannigfaltigkeiten
reduziert. Dies ist nicht-trivial, da die Gruppe
der Translationen und Rotationen. In [2] und
[3] haben wir die Dynamik in der Nähe von
Verzweigungspunkten auf endlich-dimensionale Zentrumsmannigfaltigkeiten
reduziert. Dies ist nicht-trivial, da die Gruppe 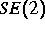 nicht kompakt
ist und auf den relevanten Funktionenräumen nicht norm-stetig
operiert. In einigen Fällen ist die Gruppenaktion sogar unstetig.
Die Gleichungen auf der Zentrumsmannigfaltigkeit besitzen eine
zusätzliche Struktur, die in [1] geklärt wurde. In
der letztgenannten Arbeit wurden darüber hinaus Bedingungen für das
Driften und Mäandern von Wellen hergeleitet. Diese Kriterien sind
numerisch leicht berechenbar. Damit konnten wir die oben beschriebenen
Phänomene durch Hopf-Verzweigungen erklären. In einer weiteren
geplanten Arbeit wollen wir diese Techniken auf sekundäre
Bifurkationen zu Tori mit drei Frequenzen anwenden, die ebenfalls
experimentell beobachtet worden sind.
nicht kompakt
ist und auf den relevanten Funktionenräumen nicht norm-stetig
operiert. In einigen Fällen ist die Gruppenaktion sogar unstetig.
Die Gleichungen auf der Zentrumsmannigfaltigkeit besitzen eine
zusätzliche Struktur, die in [1] geklärt wurde. In
der letztgenannten Arbeit wurden darüber hinaus Bedingungen für das
Driften und Mäandern von Wellen hergeleitet. Diese Kriterien sind
numerisch leicht berechenbar. Damit konnten wir die oben beschriebenen
Phänomene durch Hopf-Verzweigungen erklären. In einer weiteren
geplanten Arbeit wollen wir diese Techniken auf sekundäre
Bifurkationen zu Tori mit drei Frequenzen anwenden, die ebenfalls
experimentell beobachtet worden sind.
Projektliteratur:
-
B. FIEDLER, B. SANDSTEDE, A. SCHEEL, C. WULFF,
Bifurcations from relative equilibria of non-compact group
actions: Skew products, meanders, and drifts,
DFG-Schwerpunktreihe, Preprint No. 55/96 (1996); Doc. Math. J. DMV,
1 (1996), pp. 479--505.
-
B. SANDSTEDE, A. SCHEEL, C. WULFF,
Center-manifold reduction for spiral waves,
erscheint in: C. R. Acad. Sci. Ser. I.
-
B. SANDSTEDE, A. SCHEEL, C. WULFF,
Dynamics of spiral waves on unbounded domains using
center-manifold reductions,
WIAS-Preprint No. 288, Berlin 1996.
-
D. ARMBRUSTER, P. CHOSSAT,
Heteroclinic cycles in a spherically invariant system, Physica
50D (1991), pp. 155--176.
-
P. CHOSSAT, F. GUYARD, R. LAUTERBACH,
Generalized heteroclinic cycles in spherically invariant systems and their
perturbations, WIAS-Preprint No. 303, Berlin 1996.
-
P. CHOSSAT, R. LAUTERBACH, I. MELBOURNE,
Steady-state bifurcation with O(3)-symmetry,
Arch. Rat. Mech. Anal., 113 (4) (1991), pp. 313--376.
-
F. GUYARD, R. LAUTERBACH,
Forced symmetry breaking perturbations for periodic solutions,
erscheint in: Nonlinearity.
-
R. LAUTERBACH, S. MAIER, E. REISSNER,
A systematic study of heteroclinic cycles in dynamical systems with
broken symmetries,
Proc. Roy. Soc., Edinburgh, 126A (1996), pp. 885--909.
-
R. LAUTERBACH, M. ROBERTS,
Heteroclinic cycles in dynamical systems with broken spherical
symmetry, J. Diff. Equat., 100 (1992), pp. 428--448.
-
D. PETERHOF,
Hydrodynamische Probleme im dünnen Kugelspalt,
Dissertation, Freie Universität Berlin, 1996.





Next: Singulär gestörte Systeme
Up:
Previous: Optimale Steuerung diskontinuierlicher
wwwadmin@wias-berlin.de
Mon Feb 17 13:38:21 MET 1997
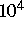 Jahren seine Orientierung
ändert. Nach einer langen Zeit stabiler Orientierung gibt es eine
vergleichsweise kurze Phase mit sehr komplizierten
Strukturen, auf die dann wieder eine lange Phase konstanter
Orientierung folgt,
allerdings mit vertauschten Polen.
Ein Zugang erklärt den sogenannten Geodynamo mit einer
Konvektionsbewegung geladener Flüssigkeiten in einer Schicht des
Erdkernes. Eine mathematische Beschreibung erfolgt mit den
Magnetohydrodynamischen Gleichungen. Ein mathematisches Objekt, das
qualitativ in der Lage ist, die obengenannten Orientierungswechsel
des Erdmagnetfeldes zu beschreiben, sind sogenannte heterokline Zyklen,
deren Existenz (oft) zur Folge hat, daß es Anfangswerte gibt, für die
die Lösung wieder in eine Umgebung des Ausgangspunktes zurückkehrt.
Solche sogenannten rekurrenten Strukturen sind typisch für das
Auftreten komplizierten dynamischen Verhaltens. Daraus ergibt sich die
natürliche Frage, ob es in dem System, das die Bewegung der
Flüssigkeit modelliert, solche heteroklinen Zykel gibt. In diesem Fall
führen die genannten Reduktionen auf gewöhnliche
Differentialgleichungen in Darstellungsräumen der Gruppe O(3). Für
solche Gleichungen ist bekannt, daß zumindest in der Nähe der
Instabilität der reinen Wärmeleitungslösung für Räume mit
irreduziblen Darstellungen keine heteroklinen Zykel existieren [6].
Solche Räume mit irreduziblen Darstellungen wären aber die natürlichen Räume für diese
Untersuchungen. Jedoch führen die Parameterwerte, die man
für das Beispiel der Erde für gegeben ansieht, auf eine
Darstellung einer Interaktion der
Jahren seine Orientierung
ändert. Nach einer langen Zeit stabiler Orientierung gibt es eine
vergleichsweise kurze Phase mit sehr komplizierten
Strukturen, auf die dann wieder eine lange Phase konstanter
Orientierung folgt,
allerdings mit vertauschten Polen.
Ein Zugang erklärt den sogenannten Geodynamo mit einer
Konvektionsbewegung geladener Flüssigkeiten in einer Schicht des
Erdkernes. Eine mathematische Beschreibung erfolgt mit den
Magnetohydrodynamischen Gleichungen. Ein mathematisches Objekt, das
qualitativ in der Lage ist, die obengenannten Orientierungswechsel
des Erdmagnetfeldes zu beschreiben, sind sogenannte heterokline Zyklen,
deren Existenz (oft) zur Folge hat, daß es Anfangswerte gibt, für die
die Lösung wieder in eine Umgebung des Ausgangspunktes zurückkehrt.
Solche sogenannten rekurrenten Strukturen sind typisch für das
Auftreten komplizierten dynamischen Verhaltens. Daraus ergibt sich die
natürliche Frage, ob es in dem System, das die Bewegung der
Flüssigkeit modelliert, solche heteroklinen Zykel gibt. In diesem Fall
führen die genannten Reduktionen auf gewöhnliche
Differentialgleichungen in Darstellungsräumen der Gruppe O(3). Für
solche Gleichungen ist bekannt, daß zumindest in der Nähe der
Instabilität der reinen Wärmeleitungslösung für Räume mit
irreduziblen Darstellungen keine heteroklinen Zykel existieren [6].
Solche Räume mit irreduziblen Darstellungen wären aber die natürlichen Räume für diese
Untersuchungen. Jedoch führen die Parameterwerte, die man
für das Beispiel der Erde für gegeben ansieht, auf eine
Darstellung einer Interaktion der 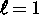 und
und 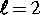 -Moden
(Kugelflächenfunktionen erster und zweiter Ordnung). Im nichtrotierenden Fall
haben Chossat und Armbruster [4] die Existenz heterokliner
Zykel in dieser Darstellung für gewisse Parameterwerte
nachgewiesen. Dieser Zykel ist allerdings nicht stabil
gegenüber Störungen, die die Symmetrie des Problems brechen (Rotation).
Methoden zur Untersuchung solcher Probleme mit erzwungener
Symmetriebrechung
gehen auf
[9] zurück. Die dort begonnenen Arbeiten wurden
innermathematisch
in [7, 8] ausgebaut. Diese Klassifizierung
zeigt, daß der aus [9] bekannte Weg, heterokline Zykel im
Fall gebrochener Symmetrien zu konstruieren, für eine Erklärung des
Verhaltens des Erdmagnetfeldes nicht geeignet ist.
Ideen, die eine Fortentwicklung der Arbeiten von Chossat und
Armbruster und von Lauterbach und Roberts sind, erlauben (unter vereinfachenden Annahmen)
in der
-Moden
(Kugelflächenfunktionen erster und zweiter Ordnung). Im nichtrotierenden Fall
haben Chossat und Armbruster [4] die Existenz heterokliner
Zykel in dieser Darstellung für gewisse Parameterwerte
nachgewiesen. Dieser Zykel ist allerdings nicht stabil
gegenüber Störungen, die die Symmetrie des Problems brechen (Rotation).
Methoden zur Untersuchung solcher Probleme mit erzwungener
Symmetriebrechung
gehen auf
[9] zurück. Die dort begonnenen Arbeiten wurden
innermathematisch
in [7, 8] ausgebaut. Diese Klassifizierung
zeigt, daß der aus [9] bekannte Weg, heterokline Zykel im
Fall gebrochener Symmetrien zu konstruieren, für eine Erklärung des
Verhaltens des Erdmagnetfeldes nicht geeignet ist.
Ideen, die eine Fortentwicklung der Arbeiten von Chossat und
Armbruster und von Lauterbach und Roberts sind, erlauben (unter vereinfachenden Annahmen)
in der 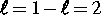 -Modeninteraktion
mit Rotation die Existenz stabiler heterokliner Zykel zu zeigen
[5].
-Modeninteraktion
mit Rotation die Existenz stabiler heterokliner Zykel zu zeigen
[5]. 




 Physikalisch bedeutungsvoll wären solche Zykel vor allem dann, wenn die
im Zyklus enthaltenen (relativen) Ruhelagen rein einmodig (
Physikalisch bedeutungsvoll wären solche Zykel vor allem dann, wenn die
im Zyklus enthaltenen (relativen) Ruhelagen rein einmodig (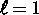 )
wären. In unseren bisherigen Untersuchungen konnten wir heterokline Zykel
und deren Stabilität nur nachweisen, wenn einmodige
)
wären. In unseren bisherigen Untersuchungen konnten wir heterokline Zykel
und deren Stabilität nur nachweisen, wenn einmodige 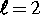 -
Gleichgewichtslagen auftreten. Unsere Untersuchungen deuten auf die
Existenz von Zyklen mit
einmodigen
-
Gleichgewichtslagen auftreten. Unsere Untersuchungen deuten auf die
Existenz von Zyklen mit
einmodigen 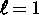 Gleichgewichten hin. Allerdings konnten dafür noch nicht
alle Beweisschritte durchgeführt
werden. Die Probleme liegen in der hohen Dimension des Parameterraumes
und der damit verbundenen Degeneriertheit des relevanten
Verzweigungsproblems. Wir vermuten jedoch, daß diese Zykel in der Nähe der
von uns beschriebenen Zykel gefunden werden können.
Gleichgewichten hin. Allerdings konnten dafür noch nicht
alle Beweisschritte durchgeführt
werden. Die Probleme liegen in der hohen Dimension des Parameterraumes
und der damit verbundenen Degeneriertheit des relevanten
Verzweigungsproblems. Wir vermuten jedoch, daß diese Zykel in der Nähe der
von uns beschriebenen Zykel gefunden werden können.
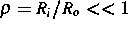 . Die Fälle
. Die Fälle 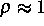 sind für Klimamodelle und
atmosphärische Vorgänge bedeutungsvoll. Allerdings kann man dieses
Problem nicht auf eine endlichdimensionale Dynamik reduzieren
[
sind für Klimamodelle und
atmosphärische Vorgänge bedeutungsvoll. Allerdings kann man dieses
Problem nicht auf eine endlichdimensionale Dynamik reduzieren
[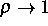 partielle
Differentialgleichungen als Grenzgleichungen betrachten. Für den Fall der
reinen Navier-Stokes Gleichungen wird die Dynamik für große
Anfangsbedingungen und Anregungen näherungsweise durch die
Navier-Stokes Gleichung auf der Kugeloberfläche beschrieben.
partielle
Differentialgleichungen als Grenzgleichungen betrachten. Für den Fall der
reinen Navier-Stokes Gleichungen wird die Dynamik für große
Anfangsbedingungen und Anregungen näherungsweise durch die
Navier-Stokes Gleichung auf der Kugeloberfläche beschrieben.
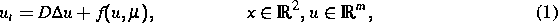
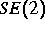 der Translationen und Rotationen. In [
der Translationen und Rotationen. In [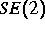 nicht kompakt
ist und auf den relevanten Funktionenräumen nicht norm-stetig
operiert. In einigen Fällen ist die Gruppenaktion sogar unstetig.
Die Gleichungen auf der Zentrumsmannigfaltigkeit besitzen eine
zusätzliche Struktur, die in [
nicht kompakt
ist und auf den relevanten Funktionenräumen nicht norm-stetig
operiert. In einigen Fällen ist die Gruppenaktion sogar unstetig.
Die Gleichungen auf der Zentrumsmannigfaltigkeit besitzen eine
zusätzliche Struktur, die in [