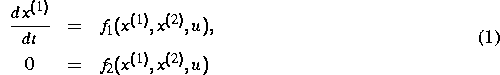
Bearbeiter: I. Bremer, W. Müller, H. Sandmann, K. R. Schneider, M. Schwarz
Kooperation: B. Hegner (BASF AG Ludwigshafen), G. Wozny (TU Berlin)
Beschreibung der Forschungsarbeit:
Die ökonomische Relevanz des Projekts und das zu seiner Bearbeitung entwickelte Konzept wurden im Jahresforschungsbericht 1995 erläutert.
Das mathematische Modell für die zu steuernden Destillationsprozesse stellt ein großes nichtlineares Algebro-Differentialgleichungssystem vom Typ
dar,
wobei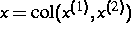 
den Vektor der
Prozeßzustandsgrößen (Stoffmengen, Konzentrationen, Drucke, Temperaturen
etc.) und u den Vektor der Steuergrößen bezeichnet, durch die von außen
auf den Prozeßverlauf Einfluß genommen werden kann. Diese
Steuergrößen können zeitlich konstante Parameter, 
,
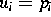oder zeitlich veränderliche Steuerfunktionen,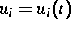 
,
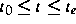, sein. Bei realen Destillationsprozessen kann das
System (1) aus Tausenden von Gleichungen bestehen.
Die Steuergrößen sind so zu wählen, daß die Lösungen noch gewisse
Zusatzbedingungen erfüllen. Typisch sind hierbei u. a. Bedingungen
der Gestalt
(Massenbedingungen) oder
(Reinheitsbedingungen) für diejenigen Teilabschnitte des
Prozeßablaufs, die Nutzfraktionen darstellen.
Die Zeitpunkte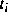 
, 
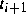sind Umschaltzeiten und somit ebenfalls
Steuergrößen.
Das Optimalsteuerungsproblem läßt sich dann in der Form
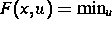unter den Nebenbedingungen (1),
(2),
(3) und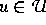 
schreiben. Dabei ist F ein vorgegebenes
Zielfunktional (z. B. größte Ausbeute bei vorgegebener Prozeßlaufzeit
oder kleinste Prozeßlaufzeit bei vorgeschriebener Ausbeute
oder ,,Profit`` = Ausbeute/Prozeßlaufzeit), und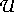 
bezeichnet die Menge der zulässigen Steuerungen.
Die Steuerungen werden
durch Elemente
eines geeigneten Funktionensystems (z. B.
stückweise lineare Funktionen oder Splines) approximiert.
Auf diese Weise wird das
Optimalsteuerungsproblem in ein endlich- (aber i. a. sehr
hoch-) dimensionales nichtlineares Optimierungsproblem
überführt.
Im Berichtszeitraum wurden folgende Probleme bearbeitet.
Weiterentwicklung des Simulators. Bei der Gewinnung zuverlässiger Lösungen für den Optimierungsprozeß muß der Simulator auch unter extremen Bedingungen (ungünstige Fahrweisen der Destillationsanlage) arbeiten. In enger Zusammenarbeit mit dem Kooperationspartner konnte die Robustheit des Simulators entscheidend verbessert werden.
Black-box-Optimierung produktionsrelevanter Batchprozesse. Unter Verwendung produktionsrelevanter Daten des Kooperationspartners wurden durch direkte Kombination des Simulators mit einem SQP-Optimierungsalgorithmus Vorschläge zur Verbesserung der Prozeßsteuerung erarbeitet (siehe Abb. 1). Gleichzeitig ergaben sich Hinweise zur Verbesserung des Simulators.
Optimierung von Batch-Destillation mit Recycling. Falls die Abfallprodukte einer Batch-Destillation dem Rohmaterial der folgenden Charge hinzugefügt werden, spricht man von Recycling. Unter Verwendung der Black-Box-Optimierung konnten für eine optimale Fahrweise von unstetiger Destillation mit Recycling erste Resultate gewonnen werden.
Interne Differentiation. Bisher wurden die benötigten Gradienten für die Optimierung numerisch approximiert. Dadurch wird die Leistungsfähigkeit der SQP-Verfahren begrenzt. Zur analytischen Berechnung der Gradienten des diskretisierten Systems wird zu (1) das entsprechende lineare Variationssystem bezüglich der Steuerung u hinzugefügt und synchron behandelt (Verfahren der internen Differentiation).
