Bearbeiter: I. Bremer, R. Antonova
Kooperation: U. Pallaske (Bayer AG, Leverkusen)
Förderung: BMBF-Förderprogramm ,,Anwendungsorientierte Verbundvorhaben auf dem Gebiet der Mathematik``
Beschreibung der Forschungsarbeit:
Der Gegenstand der Untersuchungen ist eine effiziente Simulation der Dynamik von Polymerisationsprozessen mit mehreren unterschiedlichen Monomeren im Semibatch-Betrieb. Diese Simulationen werden beim Projektpartner verwendet, um aus Massen- bzw. Molekulargewichtsverteilungen von eingebauten Monomeren Aussagen über die zu erwartende Qualität des Produktes abzuleiten.
Für den Semibatch-Betrieb ist kennzeichnend, daß die Verteilungen der zeitlichen Ableitungen der Molekulargewichte eine wesentlich geringere Komplexität als die Verteilungen der Molekulargewichte aufweisen. Deswegen kommt die endlichdimensionale Approximation der ,,differentiellen`` Verteilungen mit wesentlich weniger Gleichungen aus als eine direkte Approximation der gesuchten Verteilungen. Das macht den Ansatz in [3] als Ausgangspunkt wieder interessant. Wir verwenden
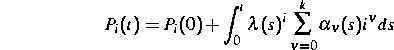
zur Approximation des Molekulargewichts des Polymers der Kettenlänge
i zum Zeitpunkt t.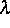 
, k und 
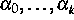sind zu bestimmen.
Bei mehreren beteiligten Monomerspezies sind räumlich mehrdimensionale (diskrete) Verteilungen zu approximieren. Wir summieren zunächst die Molekulargewichtskonzentrationen für gleiche Kettenlängen auf und benutzen für die so erhaltene Verteilung den obigen eindimensionalen Ansatz. Den mehrdimensionalen Ansatz bekommen wir dann aus dem Produkt des eindimensionalen Ansatzes mit einer geeigneten mehrdimensionalen Verteilung:
In [1] wurde dargelegt, wie u. a. mit Hilfe des
Galerkinansatzes und der Momentemethode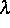 
, k und die
Koeffizienten 
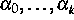bestimmt werden. Die zur Berechnung
notwendigen Gleichungen werden nicht unmittelbar gelöst, sondern als
Kontrollproblem formuliert und während der Simulation mitgeführt.
Die Gleichungen für das Momentesystem werden von einem chemischen Compiler aus der Reaktionskinetik abgeleitet. Es wurde eine Sprache entwickelt, die eine kompakte Notation der Reaktionskinetik unabhängig von der Zahl der beteiligten Monomere ermöglicht. Die Ausgabe erfolgt entsprechend der vorhandenen Simulationsumgebung, z. B. als Fortrancode. Über eine plattformunabhängige graphische Oberfläche ist die Benutzerführung von der Eingabe der Reaktionskinetik bis zur Simulation und Visualisierung der Ergebnisse möglich.
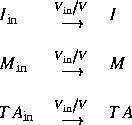
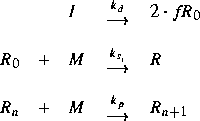
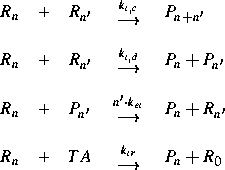
Die Kettenlänge wurde für die Darstellung logarithmisch skaliert.
Projektliteratur:
