




Next: Projektionsverfahren zur Simulation
Up:
Previous:
Bearbeiter: U. Bandelow,
R. Lauterbach,
D. Peterhof,
L. Recke,
B. Sandstede
Kooperation:
J. C. Alexander, M. N. Grillakis (Department of Mathematics, University
of Maryland, USA), C. K. R. T. Jones (Division of Applied Mathematics, Brown
University, USA), E. Patzak, B. Sartorius (Heinrich-Hertz-Institut für
Nachrichtentechnik Berlin), H.-J. Wünsche (Institut für Physik der
Humboldt-Universität zu Berlin)
Förderung: DFG, Schwerpunktprogramm ,,Strukturbildung in
dissipativen Systemen: Experiment und Theorie im qualitativen
Vergleich``
Feodor-Lynen Stipendium der Alexander von Humboldt-Stiftung
Beschreibung der Forschungsarbeit:
In optischen Kommunikationssystemen werden optische Fasern benutzt, um
Bit-Pakete schnell und zuverlässig über lange Distanzen hinweg
übertragen zu können. Der Einsatz optischer Fasern in
transatlantischen Kommunikationssystemen hängt wesentlich davon ab,
ob der auftretenden Dämpfung entgegengewirkt werden kann und Signale
somit ungestört übermittelt werden. Zugleich sollten die einzelnen
Informationsbits im Signal möglichst dicht aufeinanderfolgen.
Um optische Fasern optimal ausnutzen zu können, sollten die
Bit-Pakete im Empfänger mit optischen anstatt mit elektronischen
Komponenten regeneriert werden. Dazu müssen unter anderem Modulations-
und Trägerfrequenzen des Signals zurückgewonnen und anschließend
die Frequenz der optischen Empfänger-Komponente synchronisiert
werden.
1. Übertragung von Pulspaketen in optischen Fasern mit
Phasen-sensitiven Verstärkern
In [4] wurde vorgeschlagen, phasensensitive
Verstärker zu benutzen, um eine ungestörte Übertragung von Signalen
in optischen Fasern zu garantieren. Weiterhin wurde in
[4] formal eine Modellgleichung zur Beschreibung
optischer Fasern unter dem Einfluß derartiger Verstärker hergeleitet
und die Existenz eines stabilen 1-Pulses für sehr kleine
Verstärkerdistanzen gezeigt. Der 1-Puls entspricht der Übertragung
eines einzelnen Informationsbits.
Wir haben zunächst in [1] gezeigt, daß der 1-Puls
tatsächlich stabil über einen großen Parameterbereich hinweg ist.
Interessant sind dann Existenz und Stabilität von N-Pulsen, die der
Übertragung mehrerer Informationsbits entsprechen. Motiviert durch
dieses Problem wurde in [8] erstmals die Stabilität
derartiger Lösungen untersucht, und es wurden allgemeine Kriterien entwickelt,
die Stabilität garantieren. Anschließend haben wir in
[9] für die Modellgleichung die Existenz von stabilen
N-Pulsen für jedes N nachgewiesen. Dazu haben wir sogenannte
reversible Orbit-flip Verzweigungen in einem abstrakten Kontext
untersucht und das Resultat dann konkret auf die Modellgleichung
angewendet. Sämtliche Voraussetzungen konnten analytisch für die
Modellgleichung nachgewiesen werden. Stabilität der N-Pulse wurde
mit der in [8] entwickelten Methode gezeigt. Zuletzt
wurde die Modellgleichung mit numerischen Simulationen außerhalb des
Parameterbereiches untersucht, in dem unsere analytischen Resultate
gültig sind.
2. Regeneration von optischen Signalen mit Hilfe von
Halbleiterlasern
Die Regeneration eines optischen Signales bedarf eines
Entscheiderbauelementes, das den Takt des Signales erkennt und im
richtigen Moment die Information abfragt. Eine
optoelektronische Lösung dieser Aufgabenstellung wurde von
Sartorius et al. am Heinrich-Hertz-Institut vorgeschlagen.
Sie beruht auf den Selbstpulsationen, die kürzlich in
Mehrsektions-DFB-Halbleiterlasern gefunden wurden.
Wir untersuchen mathematische Modelle (Randwertprobleme für
hyperbolische Systeme erster Ordnung; gewöhnliche
Differentialgleichungen, deren rechte Seiten implizit durch
Sturm-Liouville Eigenwertprobleme gegeben sind), die das dynamische
Verhalten von gerade diesen Mehrsektions-DFB-Halbleiterlasern beschreiben.
Aus Sicht der Mathematik führt das Problem der
Rückgewinnung der Signale auf Locking-Phänomene und erzwungene
Symmetriebrechungen von rotierenden oder modulierten Wellen.
Im Laufe des letzten Jahres wurde die betrachtete Modellklasse durch
Hinzunahme einer zusätzlichen Phasensteuersektion und die
Berücksichtigung thermischer Effekte erweitert.
Dabei wurden folgende Themen bearbeitet:
Selbstpulsationen.
Selbstpulsationen sind modulierte Wellen, die durch Hopf-Bifurkationen
aus rotierenden Wellen entstehen. Wesentliche Charakteristika dieser
Lösungen wurden beschrieben, so zum Beispiel der Bereich der
Laserparameter, in dem die Selbstpulsationen auftreten, ihre Träger-
und Repetitionsfrequenz, sowie ihre Amplitude und Stabilität.
Vergleiche zwischen experimentellen und numerischen Ergebnissen, die
von den Kooperationspartnern angestellt wurden, ergaben eine sehr gute
Übereinstimmung.
Taktrückgewinnung.
Aus mathematischer Sicht geht es hierbei um die Synchronisation der
modulierten Welle unter Einwirkung einer externen, die Symmetrie und
die Autonomie brechenden Störung vom gleichen Typ. Wir haben die
Locking-Bereiche im
Raum der Laser- und Signalparameter, sowie die Anzahl und die Stabilität der
synchronisierten Lösungen analytisch beschrieben. Eine numerische
Realisierung der entsprechenden Algorithmen ist derzeitig in
Arbeit.
Erzeugung von Laserpulsationen durch Injektion optischer Signale
mit zeitlich konstanter Intensität.
Die rotierenden Wellen werden durch externe Signale gleichen Typs gestört, die
die Symmetrie, aber nicht
die Autonomie des Systems brechen. Dabei entstehen
synchronisierte rotierende bzw. modulierte Wellen. Zu diesem
Thema wurden sowohl analytische Untersuchungen als auch numerische
Simulationen durchgeführt.
Singularitäten.
Die bisher bekannten Selbstpulsationen treten offenbar nur in der
Nähe von komplizierten Singularitäten auf. Physikalisch gesehen
handelt es sich um die Überlagerung zweier ,,erster
Laserschwellen`` mit
gleichen optischen Frequenzen. In den mathematischen Modellen
treten diese Überlagerungen als Singularitäten der Kodimension drei
(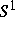 -äquivariante Hopf-Bifurkation mit zweifachem, nicht
halbeinfachem Eigenwertpaar) auf. Deshalb ist zu erwarten, daß solche
Selbstpulsationen nur bei Bauelementen mit mindestens drei
einstellbaren Parametern stabil ansteuerbar sind. Diese qualitative
Erkenntnis wurde durch die Experimente am Heinrich-Hertz-Institut
bestätigt. Dort wurde eine zusätzliche ,,Phasensteuersektion`` in einem
Zweisektions-DFB-Laser integriert, um durch Feinabstimmung des Stromes
in der zusätzlichen Sektion eine Reproduzierbarkeit der
Selbstpulsationen zu erreichen.
-äquivariante Hopf-Bifurkation mit zweifachem, nicht
halbeinfachem Eigenwertpaar) auf. Deshalb ist zu erwarten, daß solche
Selbstpulsationen nur bei Bauelementen mit mindestens drei
einstellbaren Parametern stabil ansteuerbar sind. Diese qualitative
Erkenntnis wurde durch die Experimente am Heinrich-Hertz-Institut
bestätigt. Dort wurde eine zusätzliche ,,Phasensteuersektion`` in einem
Zweisektions-DFB-Laser integriert, um durch Feinabstimmung des Stromes
in der zusätzlichen Sektion eine Reproduzierbarkeit der
Selbstpulsationen zu erreichen.
Normalform und versale Deformation der Kodimension drei Singularität
wurden aufgestellt. Derzeit wird an der physikalischen Identifikation
der Parameter und an der vollständigen Beschreibung der Dynamik nahe
der Singularität gearbeitet.
Approximationen mit zeitabhängigen Moden.
Ziel dieser Betrachtungen ist die Reduktion der partiellen
Differentialgleichung auf eine gewöhnliche Differentialgleichung.
Die rechte Seite der ODE wird allerdings implizit durch
Sturm-Liouvillesche Randwertprobleme definiert. Dabei wird
benutzt, daß die gekoppelten Wellengleichungen lineare Gleichungen
für die komplexen Feldamplituden sind, deren Koeffizienten von den
Ladungsträgerdichten abhängen. Folglich bietet sich eine Entwicklung
der komplexen Feldamplituden nach entsprechenden Eigenfunktionen und
beigeordneten Eigenfunktionen an. Diese hängen allerdings von den
Ladungsträgerdichten und damit parametrisch von der Zeit ab.
Auf dieser Grundlage wurde das Programmpaket AUTO mit einem
Programm zur Berechnung der implizit gegebenen rechten Seiten
verknüpft und auf Zwei- und Dreisektionslaser angewendet.
Die genannten Arbeiten vertiefen das Verständnis der komplexen
internen Dynamik dieser Bauelemente. Dadurch können wir unsere
Modelle den sich abzeichnenden neuen Anwendungen
(schnelles Schalten, schnelle elektrisch-optische Signalwandlung,
Solitonenerzeugung)
anpassen und neue Aufgabenfelder
erschließen. Sowohl das ursprüngliche Ziel der Datenregeneration, wie
auch diese neuen Probleme bedürfen intensiver zukünftiger Arbeit.
Projektliteratur:
-
J. C. ALEXANDER, M. N. GRILLAKIS, C. K. R. T. JONES, B. SANDSTEDE,
Stability of pulses on optical fibers with phase-sensitive
amplifiers,
erscheint in: Z. Angew. Math. Phys.
-
U. BANDELOW, H. J. WÜNSCHE, B. SARTORIUS, M. MÖHRLE,
Dispersive self-Q-switching in DFB Lasers - Theory versus
Experiment, erscheint in: Proceedings of 15th IEEE Int.
Semiconductor Laser Conference, eingereicht bei: IEEE Journal of Quantum Electronics.
-
U. BANDELOW, H.-J. WÜNSCHE, R. SCHATZ,
A correct single-mode photon rate equation for multi-section
lasers, IEEE Photon. Technol. Lett., Vol. 8 (1996), pp. 614--617.
-
J. N. KUTZ, C. V. HILE, W. L. KATH, R.-D. LI, P. KUMAR,
Pulse propagation in nonlinear optical fiber-lines that
employ phase-sensitive parametric amplifiers,
J. Opt. Soc. Am. B 11 (1994), pp. 2112--2123.
-
D. PETERHOF, L. RECKE, B. SANDSTEDE,
On frequency locking of self-pulsating two-section DFB lasers,
in ``Self-Organization in Activator-Inhibitor-Systems: Semiconductors,
Gas-Discharge and Chemical Active Media'', Contributions to the
157
 WE-Heraeus-Seminar, H. Engel, F.-J. Niedernostheide, H.-G.
Purwins, and E. Schöll, (Hrsg.), pp. 218--222, Wissenschaft &
Technik Verlag, Berlin, 1996.
WE-Heraeus-Seminar, H. Engel, F.-J. Niedernostheide, H.-G.
Purwins, and E. Schöll, (Hrsg.), pp. 218--222, Wissenschaft &
Technik Verlag, Berlin, 1996.
-
L. RECKE, D. PETERHOF,
Abstract forced symmetry breaking, WIAS-Preprint No. 256, Berlin
1996.
-
L. RECKE, D. PETERHOF,
Forced frequency locking in S
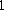 -equivariant differential
equations, WIAS-Preprint No. 257, Berlin 1996.
-equivariant differential
equations, WIAS-Preprint No. 257, Berlin 1996.
-
B. SANDSTEDE,
Stability of multiple-pulse solutions,
erscheint in: Trans. Amer. Math. Soc.
-
B. SANDSTEDE, C. K. R. T. JONES, J. C. ALEXANDER,
Existence and stability of N-pulses on optical fibers with
phase-sensitive amplifiers,
erscheint in: Physica D.
-
B. SARTORIUS, M. MÖHRLE, S. REICHENBACHER, H. PREIER, H. J. WÜNSCHE, U. BANDELOW,
Dispersive self-Q-switching in DFB Lasers,
erscheint in: IEEE Journal of Quantum Electronics.
-
H. WENZEL, U. BANDELOW, H.-J. WÜNSCHE, J. REHBERG,
Mechanisms of fast self pulsations in two-section DFB lasers,
IEEE Journal of Quantum Electronics QE-32, No.1 (1996), pp. 69-79.






Next: Projektionsverfahren zur Simulation
Up:
Previous:
wwwadmin@wias-berlin.de
Mon Feb 17 13:38:21 MET 1997
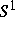 -äquivariante Hopf-Bifurkation mit zweifachem, nicht
halbeinfachem Eigenwertpaar) auf. Deshalb ist zu erwarten, daß solche
Selbstpulsationen nur bei Bauelementen mit mindestens drei
einstellbaren Parametern stabil ansteuerbar sind. Diese qualitative
Erkenntnis wurde durch die Experimente am Heinrich-Hertz-Institut
bestätigt. Dort wurde eine zusätzliche ,,Phasensteuersektion`` in einem
Zweisektions-DFB-Laser integriert, um durch Feinabstimmung des Stromes
in der zusätzlichen Sektion eine Reproduzierbarkeit der
Selbstpulsationen zu erreichen.
-äquivariante Hopf-Bifurkation mit zweifachem, nicht
halbeinfachem Eigenwertpaar) auf. Deshalb ist zu erwarten, daß solche
Selbstpulsationen nur bei Bauelementen mit mindestens drei
einstellbaren Parametern stabil ansteuerbar sind. Diese qualitative
Erkenntnis wurde durch die Experimente am Heinrich-Hertz-Institut
bestätigt. Dort wurde eine zusätzliche ,,Phasensteuersektion`` in einem
Zweisektions-DFB-Laser integriert, um durch Feinabstimmung des Stromes
in der zusätzlichen Sektion eine Reproduzierbarkeit der
Selbstpulsationen zu erreichen.





 WE-Heraeus-Seminar, H. Engel, F.-J. Niedernostheide, H.-G.
Purwins, and E. Schöll, (Hrsg.), pp. 218--222, Wissenschaft &
Technik Verlag, Berlin, 1996.
WE-Heraeus-Seminar, H. Engel, F.-J. Niedernostheide, H.-G.
Purwins, and E. Schöll, (Hrsg.), pp. 218--222, Wissenschaft &
Technik Verlag, Berlin, 1996.
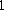 -equivariant differential
equations, WIAS-Preprint No. 257, Berlin 1996.
-equivariant differential
equations, WIAS-Preprint No. 257, Berlin 1996.

