



Next: Randintegralgleichungen und die
Up:
Previous: Multiskalen-Vorkonditionierer und optimale
Bearbeiter: A. Rathsfeld
Kooperation: R. Klees (Delft University of Technology)
Beschreibung der Forschungsarbeit:
Ein klassisches Grundproblem der Geodäsie besteht in der Bestimmung
des Schwerefeldes der Erde aus gemessenen Schwerewerten über der als
bekannt vorausgesetzten Erdoberfläche. Mathematisch bedeutet dies die
Lösung der Poisson-Gleichung mit einer nichtlinearen
Randbedingung. Führt man nun ein gut approximierendes Vergleichsfeld
ein und vernachlässigt man Glieder kleiner Ordnung, so kann das
Randwertproblem auf das lineare Problem der schiefen Ableitung für
die Laplace-Gleichung zurückgeführt werden.
Dieses Problem wird mittels
Randelementtechnik diskretisiert und numerisch gelöst. Dabei
entstehen große Systeme linearer Gleichungen mit vollbesetzten
Matrizen, deren Aufstellung und Lösung viel Rechenzeit und
Speicherplatz erfordert. Als alternatives Verfahren haben wir einen
Waveletalgorithmus entwickelt (vgl. [1]), bei dem 95 % der
Einträge in der 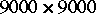 Matrix vernachlässigt werden
können. Wenn die Matrix mit einem geeigneten Quadraturverfahren
berechnet und das Gleichungssystem iterativ gelöst wird, dann kann
die Gesamtrechenzeit für ein
Matrix vernachlässigt werden
können. Wenn die Matrix mit einem geeigneten Quadraturverfahren
berechnet und das Gleichungssystem iterativ gelöst wird, dann kann
die Gesamtrechenzeit für ein 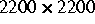 System auf 53 % der
Zeit für herkömmliche Verfahren reduziert werden. Es hat sich also
gezeigt, daß die bekannten theoretischen Resultate von Dahmen,
Prößdorf und Schneider [2] für einfache Modellprobleme
auch im Fall komplizierter Geometrien aus praktisch relevanten Anwendungen von
großem Nutzen sind.
System auf 53 % der
Zeit für herkömmliche Verfahren reduziert werden. Es hat sich also
gezeigt, daß die bekannten theoretischen Resultate von Dahmen,
Prößdorf und Schneider [2] für einfache Modellprobleme
auch im Fall komplizierter Geometrien aus praktisch relevanten Anwendungen von
großem Nutzen sind.


Projektliteratur:
- A. RATHSFELD,
A wavelet algorithm for the boundary element solution of
a geodetic boundary value problem, in Vorbereitung.
- W. DAHMEN, S. PRÖSSDORF, R. SCHNEIDER,
Wavelet approximation methods for pseudodifferential equations II:
Matrix compression and fast solution, Advances in Computational
Mathematics, 1 (1993), 259-335.
Group_of_Office
Mon May 13 20:25:53 MET DST 1996
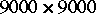 Matrix vernachlässigt werden
können. Wenn die Matrix mit einem geeigneten Quadraturverfahren
berechnet und das Gleichungssystem iterativ gelöst wird, dann kann
die Gesamtrechenzeit für ein
Matrix vernachlässigt werden
können. Wenn die Matrix mit einem geeigneten Quadraturverfahren
berechnet und das Gleichungssystem iterativ gelöst wird, dann kann
die Gesamtrechenzeit für ein 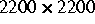 System auf 53 % der
Zeit für herkömmliche Verfahren reduziert werden. Es hat sich also
gezeigt, daß die bekannten theoretischen Resultate von Dahmen,
Prößdorf und Schneider [2] für einfache Modellprobleme
auch im Fall komplizierter Geometrien aus praktisch relevanten Anwendungen von
großem Nutzen sind.
System auf 53 % der
Zeit für herkömmliche Verfahren reduziert werden. Es hat sich also
gezeigt, daß die bekannten theoretischen Resultate von Dahmen,
Prößdorf und Schneider [2] für einfache Modellprobleme
auch im Fall komplizierter Geometrien aus praktisch relevanten Anwendungen von
großem Nutzen sind.





