



Next: Ein
Waveletalgorithmus zur
Up:
Previous: Kollokations-Randelement-Methoden mit nicht
Bearbeiter: S. Prößdorf
Kooperation: B. N. Khoromskij (Joint Institute for Nuclear Research,
Dubna, Rußland)
Beschreibung der Forschungsarbeit:
In diesem Projekt werden einige Strategien zur Konstruktion
asymptotisch optimaler Algorithmen zur Lösung von
Randintegralgleichungen für innere und äußere Randwertprobleme für
die Laplace-Gleichung über polygonalen Gebieten entwickelt und
analysiert. Das innere Dirichlet- oder Neumann-Problem ist bekanntlich
equivalent zur direkten Behandlung der Dirichlet-Neumann-Abbildung
oder deren Inversen, d. h. des Poincaré-Steklov (PS)-Operators. Zur
Konstruktion eines schnellen Algorithmus für den diskreten
PS-Operator wenden wir, im Falle von polygonalen Gebieten, die aus
Rechtecken und regulären Dreiecken zusammengesetzt sind, den
Multiskalen-Vorkonditionierer nach Bramble-Pasciak-Xu auf das
equivalente Interface-Problem in 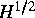 an. Ein schneller
Matrix-Vektor-Multiplikationsalgorithmus basiert auf der
Frequenz-Abschneidetechnik, angewandt auf die lokalen
Schur-Komplemente. Das vorgeschlagene Kompressionsschema für den
diskreten inneren PS-Operator hat die Komplexität
an. Ein schneller
Matrix-Vektor-Multiplikationsalgorithmus basiert auf der
Frequenz-Abschneidetechnik, angewandt auf die lokalen
Schur-Komplemente. Das vorgeschlagene Kompressionsschema für den
diskreten inneren PS-Operator hat die Komplexität 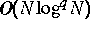 ,
, 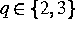 , mit einem Speicherbedarf von
, mit einem Speicherbedarf von 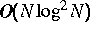 , wobei N
die Anzahl der Freiheitsgrade auf dem polygonalen Rand ist. Im Falle
des äußeren Problems schlagen wir eine Modifikation der direkten
Standard-Randelementmethode vor, deren Implementierung sich reduziert
auf eine Wavelet-Approximation entweder des Einfachschichtpotentials
oder des hypersingulären harmonischen Potentials sowie auf eine
Matrix-Vektor-Multiplikation für den diskreten inneren PS-Operator.
, wobei N
die Anzahl der Freiheitsgrade auf dem polygonalen Rand ist. Im Falle
des äußeren Problems schlagen wir eine Modifikation der direkten
Standard-Randelementmethode vor, deren Implementierung sich reduziert
auf eine Wavelet-Approximation entweder des Einfachschichtpotentials
oder des hypersingulären harmonischen Potentials sowie auf eine
Matrix-Vektor-Multiplikation für den diskreten inneren PS-Operator.
Projektliteratur:
- B. N. KHOROMSKIJ, S. PRÖSSDORF, Multilevel preconditioning
on the refined interface and optimal boundary solvers for the
Laplace equation, Advances in Computational Mathematics 4
(1995), 331--355.
Group_of_Office
Mon May 13 20:25:53 MET DST 1996
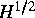 an. Ein schneller
Matrix-Vektor-Multiplikationsalgorithmus basiert auf der
Frequenz-Abschneidetechnik, angewandt auf die lokalen
Schur-Komplemente. Das vorgeschlagene Kompressionsschema für den
diskreten inneren PS-Operator hat die Komplexität
an. Ein schneller
Matrix-Vektor-Multiplikationsalgorithmus basiert auf der
Frequenz-Abschneidetechnik, angewandt auf die lokalen
Schur-Komplemente. Das vorgeschlagene Kompressionsschema für den
diskreten inneren PS-Operator hat die Komplexität 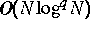 ,
, 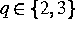 , mit einem Speicherbedarf von
, mit einem Speicherbedarf von 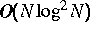 , wobei N
die Anzahl der Freiheitsgrade auf dem polygonalen Rand ist. Im Falle
des äußeren Problems schlagen wir eine Modifikation der direkten
Standard-Randelementmethode vor, deren Implementierung sich reduziert
auf eine Wavelet-Approximation entweder des Einfachschichtpotentials
oder des hypersingulären harmonischen Potentials sowie auf eine
Matrix-Vektor-Multiplikation für den diskreten inneren PS-Operator.
, wobei N
die Anzahl der Freiheitsgrade auf dem polygonalen Rand ist. Im Falle
des äußeren Problems schlagen wir eine Modifikation der direkten
Standard-Randelementmethode vor, deren Implementierung sich reduziert
auf eine Wavelet-Approximation entweder des Einfachschichtpotentials
oder des hypersingulären harmonischen Potentials sowie auf eine
Matrix-Vektor-Multiplikation für den diskreten inneren PS-Operator.



