Multiskalen-Methoden zur numerischen Behandlung von Operatorgleichungen

Bearbeiter: A. Kunoth, S. Prößdorf

Förderung: DFG

Kooperation: W. Dahmen (RWTH Aachen), R. Schneider (TH Darmstadt), K. Urban (RWTH Aachen)

Beschreibung der Forschungsarbeit:

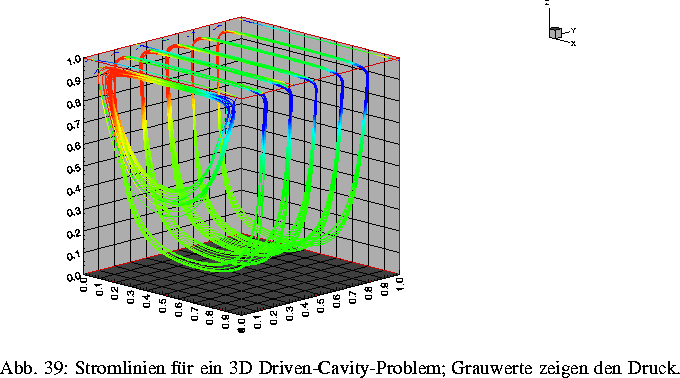
Im Rahmen des Projekts wurde schwerpunktmäßig an Multiskalenmethoden zur numerischen Behandlung von partiellen Differentialgleichungen gearbeitet. Unter Benutzung von Methoden aus der Theorie der Funktionenräume und der Approximationstheorie wurde gezeigt, wie sich optimale Vorkonditionierer für instationäre Stokes-Probleme herleiten lassen [1]. Dies zieht die iterative Lösung der entsprechenden Gleichungssysteme in optimal linearer Komplexität nach sich, was besonders höherdimensionale Probleme erst rechenbar machen läßt. Des weiteren wurde die Flexibilität von biorthogonalen Wavelets dahingehend ausgenutzt, stabile Basen im Sinne der Ladysenskaja-Babuska-Brezzi-Bedingung für Stokes-Probleme in beliebiger Dimension zu konstruieren, was bei klassischen Finite Elementen sehr schwierig sein kann. Die in [1] zu findenden entsprechenden Ergebnisse in 3D basieren zum Teil auf der Implementierung [4] und wurden in [5] detailliert beschrieben. Abb. 1 zeigt die Lösung eines Driven--Cavity Problems auf einem dreidimensionalen Einheitswürfel.

Die theoretischen, bisher lückenhaften Ergebnisse zur Konstruktion von dazu benötigten stabilen biorthogonalen Wavelets auf einem Intervall werden gegenwärtig in [2] mit einer Implementierung verschiedener, auf B-Splines beruhender Beispiele zusammengestellt. Des weiteren wurde mit [3] ein umfassender Überblick über die Verwendung wavelet-artiger Basen zur komplexitätsoptimalen Lösung von partiellen Differentialgleichungen und Integralgleichungen erstellt, in dem besonders auf die Konstruktion stabiler Wavelet-Basen auf 2D-Polyeder-Oberflächen, auf adaptive Quadratur und wavelet-basierende Fehlerschätzer eingegangen wird.

Projektliteratur:

1.   W. DAHMEN, A. KUNOTH, K. URBAN, A wavelet-Galerkin method for the Stokes equations, Technical Report ISC-95-05-MATH, Institute for Scientific Computation, Texas A&M University, Revised version, August 1995, erscheint in: Computing.

2.   W. DAHMEN, A. KUNOTH, K. URBAN, Biorthogonal spline wavelets on the interval -- Stability and moment conditions, in Vorbereitung.

3.   W. DAHMEN, A. KUNOTH, R. SCHNEIDER, Operator equations, multiscale concepts and complexity, WIAS-Preprint No. 206, Berlin 1995, erscheint in: Lectures in Applied Mathematics, J. Renegar, M. Shub and S. Smale (eds.), American Mathematical Society.

4.   A. KUNOTH, Computing integrals of refinable functions -- Documentation of the program, Version 1.1, Technical Report ISC-95-02-MATH, Institute for Scientific Computation, Texas A&M University, Mai 1995.

5.   K. URBAN, Multiskalenverfahren für das Stokes-Problem und angepaßte Wavelet-Basen, Dissertation, RWTH Aachen, 1995, erscheint in: Aachener Beiträge zur Mathematik, Augustinus-Verlag, Aachen.