



Bearbeiter: S. Prößdorf
Kooperation: G. Chiocchia, D. Tordella (Dept. of Aerospace Engineering, Politecnico di Torino)
Beschreibung der Forschungsarbeit:
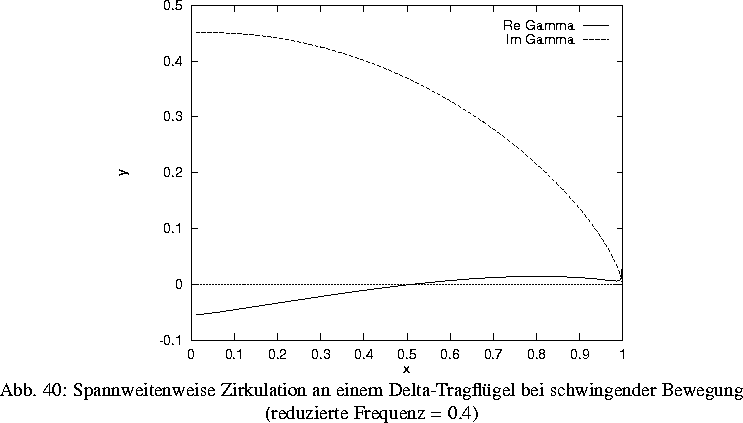
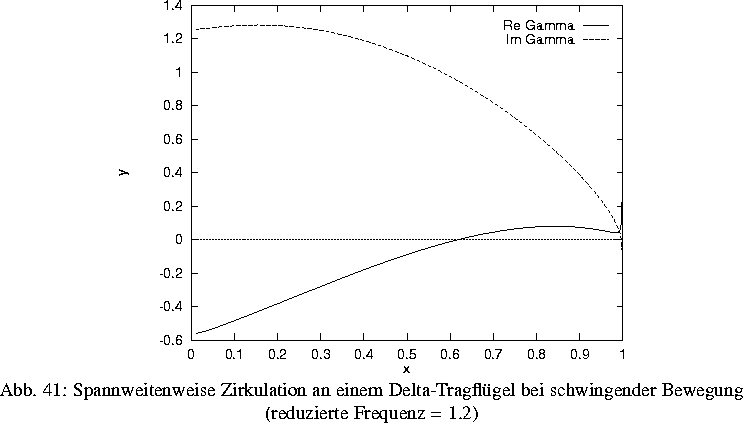
In diesem Projekt wurde eine neue Methode der nicht stationären linearen tragenden Linie zur Bestimmung der Zirkulation und der Auftriebsverteilung entlang der Spannweite eines gekrümmten Tragflügels unter den Bedingungen harmonischer Schwingungen kleiner Amplituden entwickelt. Die Methode beruht auf der sogenannten Dreiviertelpunktmethode von Pistolesi-Weissinger und deren Kopplung mit der nicht stationären Theorie von Possio für die Bewegung von Tragflächen. Dies führt auf eine singuläre Integro-Differentialgleichung vom modifizierten Prandtl'schen Typ. Diese Gleichung wird eingehend analysiert, insbesondere werden alle Singularitäten der verschiedenen Kernfunktionen, die für die Lösung der Gleichung von entscheidender Bedeutung sind, untersucht. Die Singularitäten hängen entscheidend von der geometrischen Form des Tragflügels und den physikalischen Strömungsparametern ab. Die numerische Lösungsmethode ist eine auf Tschebyscheffscher polynomialer Approximation für die gesuchte Lösung beruhende Kollokation unter Benutzung der Gauss'schen Quadraturtechnik. Für dieses Verfahren werden Stabilität und Fehlerabschätzungen in gewichteten Sobolev--Normen und in gewichteten gleichmäßigen Normen bewiesen.
Die Methode wurde für verschiedene geometrische und kinematische Tragflügelkonfigurationen numerisch getestet. Vergleiche mit bekannten Lösungen, die auf der Theorie der tragenden Fläche basieren (siehe B. Laschka) zeigten die Effizienz der Methode besonders im Falle harmonischer Schwingungen sowie in den Fällen langsamer und moderat schneller pulsierender Bewegungen. Außerdem konnte die Anwendbarkeit der Methode im Falle halbmondförmiger Flügel nachgewiesen werden, für den es in der Literatur bisher keinerlei Ergebnisse gab. Die Methode läßt weitere Anwendungen z. B. für Vorabschätzungen des aerodynamischen Verhaltens von Tragflügeln oder in der Physik der Fortbewegung von Tieren (u. a. Vogelflüge) zu.

Projektliteratur:



