Bearbeiter: B. Kleemann, S. Prößdorf
Förderung: DFG
Kooperation: W. Dahmen (RWTH Aachen), R. Schneider (TH Darmstadt), Ch. Schwab (ETH Zürich)
Beschreibung der Forschungsarbeit:
Das äußere Dirichlet Problem für die Helmholtzgleichung führt nach einem Einfachschichtpotentialansatz auf die folgende logarithmisch singuläre Integralgleichung erster Art ([1]):
wobei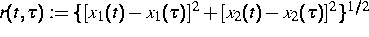 
und 
, 
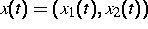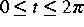die Parametrisierung
des glatten Randes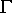 
ist.
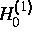bezeichnet die Hankelfunktion 0. Ordnung und 1. Art und 
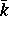die Wellenzahl.
Zur Lösung von (1) werden Wavelets zusammen mit
einem volldiskreten Kollokationsverfahren [7, 5,
6] verwendet.
Dazu werden als Ansatzfunktionen stetige,
stückweise lineare biorthogonale Wavelets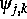 
mit zwei
verschwindenden Momenten mit folgender Maske verwendet:
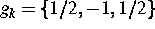. Auch diese bilden eine Rieszbasis
([8]), so daß die theoretischen Ergebnisse
von [2, 3, 4] Anwendung finden können.
Wegen der Kollokationsmethode werden auf der Testfunktionalseite
Punktauswertungen benötigt. Deshalb stellen die verwendeten
Funktionale von Brandt/Lubrecht adäquate ,,Wavelets`` im Raum der
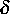-Distributionen dar.
In den Rechnungen haben beide Funktionen, sowohl die Wavelets
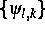als auch die Testfunktionale
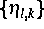, zwei verschwindende Momente, d. h., sie sind orthogonal zu
konstanten und linearen Funktionen.
Mit dem folgenden a-priori Kompressionskriterium, das in [3]
aufgestellt wurde, brauchen nur die Matrixelemente
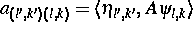berechnet und abgespeichert zu werden, die die folgende Bedingung erfüllen:
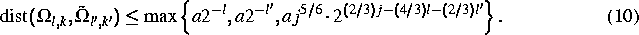
Hier bezeichnen wir mit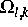 
den Träger der 
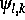, mit
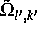den Träger der 
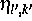, und a ist eine
Konstante, die noch geeignet gewählt werden muß. Auch für diese
Wahl kann man eine einfache und praktisch handhabbare Bedingung angeben
([6]).
Wegen des volldiskreten Verfahrens wird die
Integration mittels numerischer Quadratur realisiert.
Der Schwerpunkt des Projektes lag in der Implementierung des
Verfahrens und im Vergleich mit anderen bekannten Methoden anhand
wichtiger Testbeispiele. So wurden Beispiele mit einem Kreis, einer
Ellipse und einem tragflügelähnlichen Streuprofil für
unterschiedliche Wellenzahlen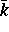 
gerechnet. Wie in der
Ingenieurliteratur üblich, wurde auch die Streuamplitude im Fernfeld
und die RCS berechnet. Dort, wo Vergleichswerte
vorlagen, konnten diese verifiziert werden. Wellenzahlen bis 10 bereiteten
keine ernsten Schwierigkeiten. Bei Wellenzahlen weit darüber hinaus
(so wurde auch mit 
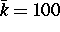gerechnet) mußte die Kompressionsrate
drastisch gesenkt und die Anzahl der Diskretisierungpunkte deutlich
erhöht werden, um noch die gewünschte Konvergenzgeschwindigkeit
zu erhalten und ein brauchbares Resultat zu erzielen.
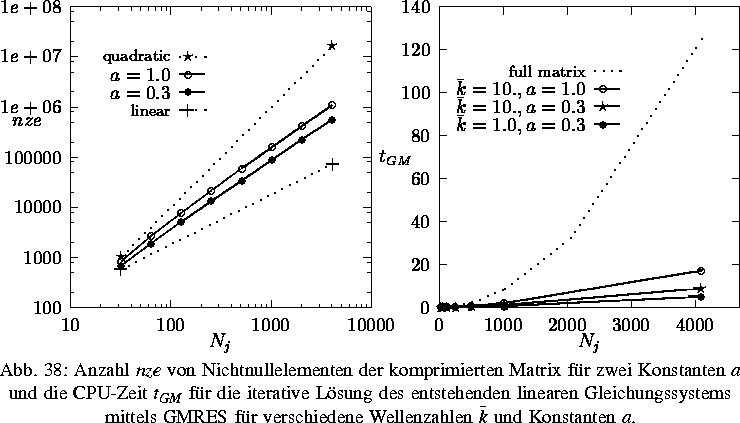
In allen Fällen erhalten wir trotz nahezu optimaler Kompressionsrate
die theoretisch zu erwartende Konvergenzordnung 2 (wegen der linearen
Ansatzfunktionen und der Trapezregel bei der Quadratur) sowohl für die
Lösung als auch für Funktionale der Lösung. So kann dieses Verfahren
aufgrund seiner Kompressionsrat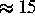en (
für N=4000)
schon für Probleme eingesetzt werden,
die mit einem üblichen Kollokationsverfahren nicht mehr behandelbar
wären.
Wie die Quadratur zu gestalten ist, um letztendlich schneller als ein übliches Diskretisierungsverfahren zu werden, wurde in [9] angegeben. Dazu wurden schon einige numerische Tests vorgenommen, die die Überlegenheit der neuen Strategie deutlich ausweisen. Dazu muß der Abstand des Trägers des Testfunktionals von dem Träger des aktuellen Wavelets, über das gerade integriert wird, bei der Quadratur mit berücksichtigt werden. Auch der Beitrag, den dieses Integral zum jeweiligen Element der Steifigkeitsmatrix leistet, hat in die Genauigkeit der durchzuführenden Quadratur einzugehen.
Projektliteratur:
