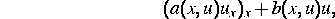




Bearbeiter: S. Handrock-Meyer
Förderung: DFG
Kooperation: M. Yamamoto (Tokio)
Beschreibung der Forschungsarbeit:
Ausserordentlich wichtig bei der Untersuchung von Koeffizientenidentifikationsproblemen ist die Beantwortung der Frage, ob die verfügbaren Meßwerte eine ausreichende Information für die Identifikation der unbekannten Parameter liefern, d. h., ob der zu bestimmende Koeffizient identifizierbar ist. Für die untersuchten Aufgaben ist die Identifizierbarkeit äquivalent zur Eindeutigkeit der Lösung des inversen Problems. Betrachtet wurden Aufgaben, die den folgenden quasilinearen Term enthalten:
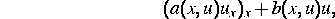
und zwar quasilineare Randwertprobleme 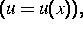 quasilineare parabolische
Anfangs-Randwertprobleme
quasilineare parabolische
Anfangs-Randwertprobleme 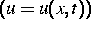 und quasilineare hyperbolische
Anfangs-Randwertprobleme
und quasilineare hyperbolische
Anfangs-Randwertprobleme 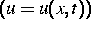 .
.
Es werden Bedingungen angegeben, unter denen jeweils einer der Koeffizienten
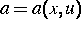 oder
oder 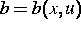 identifizierbar ist. Die erhaltenen Resultate
stellen eine Verallgemeinerung der Ergebnisse, die bekannt sind in den
Spezialfällen, in denen a bzw. b nur von der Ortsvariablen x oder nur
vom Potential u abhängen, dar. Außerdem wurde die
Identifizierbarkeitsproblematik für die drei oben formulierten Aufgaben mit
einem einheitlichen Zugang abgehandelt.
identifizierbar ist. Die erhaltenen Resultate
stellen eine Verallgemeinerung der Ergebnisse, die bekannt sind in den
Spezialfällen, in denen a bzw. b nur von der Ortsvariablen x oder nur
vom Potential u abhängen, dar. Außerdem wurde die
Identifizierbarkeitsproblematik für die drei oben formulierten Aufgaben mit
einem einheitlichen Zugang abgehandelt.
Solche Untersuchungen sind aus praktischer Sicht sinnvoll. Beispielsweise
führen eindimensionale diffusionsähnliche Systeme in einem isotropen Medium
auf eine parabolische Differentialgleichung, in welcher der Koeffizient a
gerade eine Funktion der Ortsvariablen x und des Potentials 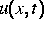 ist.
ist.
Projektliteratur: