Kooperation: L. Brüll, F. Hubbuch (Bayer AG Leverkusen), R. Zeller (Cray Research GmbH München), T. Garratt (AspenTech UK Ltd., Cambridge), U. Nowak (ZIB), O. Abel (Lehrstuhl für Prozeßtechnik, Rheinisch-Westfälische Technische Hochschule Aachen), St. Zitney (Cray Research, Inc., Eagan, USA), G. Wozny (Institut für Prozeß- und Anlagentechnik, TU Berlin)
Förderung: BMBF, im Rahmen eines Programms auf ausgewählten Gebieten anwendungsorientierter Mathematik
Beschreibung der Forschungsarbeit:
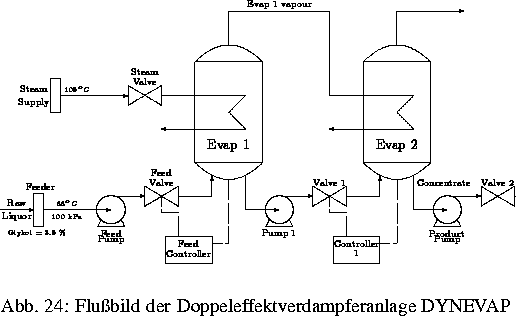
Die mathematische Modellierung verfahrenstechnischer Prozesse in der chemischen Industrie führt zu Anfangswertaufgaben für Systeme von nichtlinearen Algebro-Differentialgleichungen (DAE). Entsprechend der Modellierung chemischer Anlagen (siehe z. B. Abb. 1) ergeben sich strukturierte Systeme von DAE's. Diese Struktur wird in den von uns entwickelten numerischen Verfahren ausgenutzt. Die Algorithmen werden sowohl auf Vektorrechnern als auch auf Parallelrechnern mit distributed und shared Memory implementiert. Parallelisierungen werden auf den folgenden Niveaus des Lösungsprozesses betrachtet:
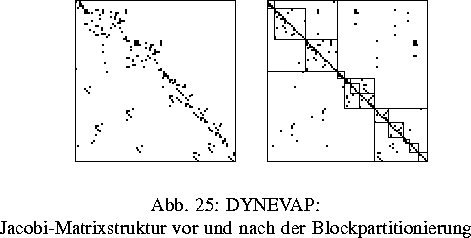
Auf dem Niveau der Differentialgleichungen werden stark gekoppelte Teilgleichungssysteme zu Blöcken zusammengefaßt und mit einem Block-Waveform-Relaxationsverfahren [1] gelöst. Dabei hat sich die Bestimmung einer Blockpartitionierung mittels Graphenalgorithmen als ein anspruchsvolles Problem herausgestellt. Es hat sich gezeigt, daß nur für eingeschränkte Aufgabenklassen eine für Waveform-Verfahren geeignete Blockpartitionierung (siehe Abb. 2) bestimmt werden kann. Für den in der Praxis wesentlichen Fall der Destillationskolonnen können wir Modellierungsrestriktionen angeben, unter denen eine solche Partitionierung existiert.
Um allgemeinere Aufgabenklassen behandeln zu können, wurde verstärkt
an einem Parallelisierungsansatz auf dem Niveau der nichtlinearen
Gleichungen gearbeitet. Dabei wird das nach Zeitdiskretisierung
entstehende nichtlineare Gleichungssystem zu einem System erweitert,
das aus Teilsystemen mit disjunkten Argumenten und einem Hauptsystem
besteht. Dieses erweiterte System wird mit einem strukturierten
Newton-Verfahren [2] gelöst, wobei die linearen Teilsysteme
parallel behandelt werden (siehe Projekt ,,Numerische Lösung
strukturierter DAE-Systeme``, S. 
). Hierzu wurde auf dem moderat
parallelen Rechner CRAY J90 ein einstufig strukturiertes
Newton-Verfahren implementiert, bei dem Teilsysteme nach rein
topologischen Kriterien (Minimierung der Anzahl der äußeren
Variablen und Erzeugung möglichst gleich großer Gleichungsblöcke)
zu Blöcken zusammengefaßt werden. Den Flaschenhals der
Parallelisierung bildet das Hauptsystem (sequentieller Anteil des
Verfahrens). Aus diesem Grund wurden von uns verschiedene
Möglichkeiten untersucht, den Rechenzeitaufwand für die Lösung des
Hauptsystems zu reduzieren [2]. Für eine Destillationsanlage mit 52
Teilsystemen wurde auf der CRAY J90 ein bezüglich der Rechenzeit
maximaler Beschleunigungsfaktor von 3,9 für acht Blöcke bei Verwendung
von acht Prozessoren erzielt [2].
Zur Lösung der Anfangswertaufgaben sind konsistente Anfangswerte zu
berechnen. Sie sind auch bei einer Reinitialisierung während der
dynamischen Simulation und für die Bestimmung stationärer Lösungen
erforderlich. Hierzu sind große schwach besetzte nichtlineare
Gleichungssysteme mit irregulärer Struktur zu behandeln. Für diese
Aufgabenklasse wurde ein zweistufiges Verfahren entwickelt (siehe
Projekt ,,Numerische Lösung schwach besetzter Systeme nichtlinearer
Gleichungen``, S. ) und auf einer CRAY T3D implementiert.
Zuerst werden mit einem Suchverfahren Startwerte für ein modifiziertes Newton-Verfahren ermittelt. Das Suchverfahren basiert auf Block-Gauß-Seidel- und Block-Gauß-Seidel-Newton-Iterationsverfahren unter Verwendung von Moore-Penrose-Pseudo-Inversen, um die unterbestimmten linearen Gleichungssysteme zu lösen, die bei der iterativen Lösung der Teilsysteme auftreten. Mit dieser Näherung wird dann ein modifiziertes gedämpftes Newton-Verfahren gestartet. Da numerisch singuläre Jacobi-Matrizen nicht auszuschließen sind, wurde das Newton-Verfahren mit einer Matrix-Analyse ausgestattet, um durch Ändern weniger Lösungskomponenten eine reguläre Jacobi-Matrix zu erhalten. --- Die schwache Besetztheit und die Strukturierung des Gleichungssystems sowie der Jacobi-Matrix werden in beiden Schritten ausgenutzt.
Die linearen Systeme mit schwach besetzten Matrizen werden mit
Sparse-Matrix-Techniken behandelt. Es werden die im Projekt
,,Numerische Lösung schwach besetzter Gleichungssysteme``
(siehe S. )
beschriebenen Verfahren eingesetzt. Die Methoden wurden an großen
Simulationsbeispielen der Bayer AG Leverkusen im Simulator SPEEDUP
erprobt, wozu uns von Cray Research die entsprechende Schnittstelle
offengelegt worden ist. Die Resultate für die Gesamtsimulation einer
Destillationskolonne TDA mit 13 436 Gleichungen und eines
Reaktormodells NIT mit 3 268 Gleichungen sind in Tabelle 1
dargelegt. Dabei ist FRONTAL ein linearer Solver in
SPEEDUP, der die Frontal-Methode benutzt, und GSPAR der von uns
entwickelte Solver.
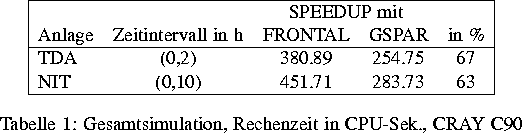
Die beträchtliche Verringerung der gesamten Simulationszeit ist dadurch zu erklären, daß GSPAR bei der Faktorisierung mit gegebener Pivotreihenfolge schneller als FRONTAL ist. Es kommt hinzu, daß GSPAR numerisch stabiler ist, weshalb weniger Faktorisierungen und Vor- und Rückwärtsrechnungen und damit weniger Newton-Schritte erforderlich sind.
Das Programm zur automatischen Erzeugung einer Schnittstelle für den DAE-Solver aus SPEEDUP-Dateien wurde weiterentwickelt. Es wird eine erweiterte Schnittstelle erzeugt, die auch datentypbezogene Initialisierungs- und Intervallgrößen enthält. Diese Größen geben einen Startwert für die Anfangswertberechnung und erlauben eine Verifikation der Lösung während der Simulation. Eine zusätzlich erzeugte Routine erlaubt die Ausgabe von Größen während der Rechnung, die durch ihre SPEEDUP-Namen identifiziert werden. Die Anpassung des Programms an die neue SPEEDUP-Version 5.5 wurde durchgeführt. Die Schnittstelle wurde für Beispiele bis zu einer Größe von 13 436 Gleichungen erzeugt und getestet.
Begonnen wurden Arbeiten zur Generierung eines Interpretercodes zur teilsystemorientierten Berechnung der Funktionswerte und Jacobi-Matrixelemente. Dieser Interpretercode wird durch Rückerkennung der Gleichungen aus den SPEEDUP-Routinen RES und DERIV erzeugt. Zur Überprüfung der Ergebnisse wurde die Ausgabe der erzeugten Gleichungen in LaTeX-Form implementiert.
Die Projektgruppe erhielt durch Unterstützung von Prof. Dr. J. Sprekels und von Cray Research, Inc., Eagan, die Autorisierung von Aspen Technology, Inc., Cambridge, USA, den Simulator SPEEDUP für fünf Jahre auf einem Cray-Rechner im ZIB für die Entwicklung numerischer Verfahren für DAE's kostenlos zu nutzen. Diese Autorisierung haben nur einige wenige Universitäten in den USA.
Für die Erprobung der linearen Solver mit SPEEDUP wurde uns ein Account auf Cray-Rechnern in Eagan, USA, mit monatlich 5 kostenlosen CPU-Stunden zur Verfügung gestellt.
Projektliteratur:
