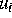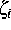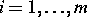Elektro-Reaktions-Diffusionssysteme in Heterostrukturen

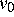Bearbeiter: A. Glitzky, K. Gröger, R. Hünlich

Kooperation: Institut für Halbleiterphysik Frankfurt (Oder) GmbH (IHP)

Beschreibung der Forschungsarbeit:

Wir behandeln im folgenden Gleichungen, die die Umverteilung elektrisch geladener Spezies in Heterostrukturen durch Diffusion und Reaktionen unter Berücksichtigung ihrer elektrischen Wechselwirkung beschreiben. Derartige Probleme entstehen beispielsweise bei der Modellierung von technologischen Prozessen zur Herstellung von Halbleiterbauelementen. Einen Überblick über derartige Modellgleichungen findet man in [9].

Ein vor allem in Simulationsprogrammen häufig benutzter Weg zur Modellierung elektrischer Wechselwirkungen ist die Annahme der lokalen Elektroneutralität. Unter dieser Annahme haben wir in [2] ein Modell mit nur einer Sorte geladener Fremdatome behandelt. Die eindeutige Lösbarkeit der Modellgleichungen, die globale Beschränktheit der Lösungen und deren exponentielles Streben zum Gleichgewicht sind nachgewiesen worden. Analoge Aussagen haben wir für ein implizites und ein semiimplizites Zeitdiskretisierungsschema erhalten. Die Konvergenz dieser Schemata ist begründet worden.

Ein anderer Weg zur Modellierung elektrischer Wechselwirkungen, der nun beschritten werden soll, besteht darin, das innere elektrische Feld mit Hilfe der Poisson-Gleichung zu berechnen. Ein allgemeines Modell für beliebig viele elektrisch geladene Spezies in Heterostrukturen führt auf ein Elektro-Reaktions-Diffusionssystem mit nichtglatten Daten. Wir bezeichnen mit 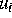, , 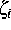, 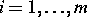die Konzentration und das elektrochemische Potential der i-ten Spezies. Das zu untersuchende Differentialgleichungssystem besteht aus m Kontinuitätsgleichungen gekoppelt mit der Poisson-Gleichung für das elektrostatische Potential :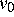

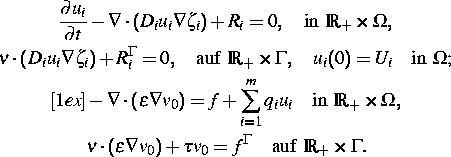
Dabei sind 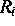bzw. 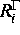die Reaktionsraten im Volumen bzw. am Rand, die ausgehend vom Massenwirkungsgesetz in der Form

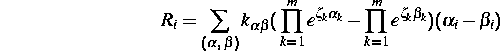
angesetzt werden. Hierbei bezeichnen 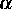und 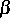die stöchiometrischen Vektoren der entsprechenden Reaktionen. Für den Zusammenhang zwischen Konzentrationen und Potentialen wird im betrachteten Modell die Boltzmann-Statistik angenommen. Die Untersuchungen erfolgen für den räumlich zweidimensionalen Fall, da Beschränktheitsaussagen für die Lösungen elliptischer Gleichungen von Gröger [8] in der Form, wie sie hier benötigt werden, nur im Zweidimensionalen verfügbar sind. Diese Beschränkung der Raumdimension ermöglicht uns aber das Anwenden und Erweitern von Einbettungsresultaten von Trudinger [10].

Unter gewissen Forderungen an die Anfangswerte 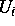und die Struktur des Reaktionssystems besitzt die Aufgabe genau einen stationären Zustand innerhalb einer Kompatibilitätsklasse, die durch den Anfangswert charakterisiert wird. Zum Beweis werden Aussagen der konvexen Analysis für Minimumprobleme strikt konvexer Funktionale herangezogen.

Ausgangspunkt für die Untersuchungen des instationären Problems sind physikalisch motivierte Abschätzungen der freien Energie

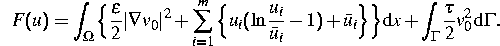
Zunächst wird gezeigt, daß die freie Energie entlang von Trajektorien des Systems monoton fällt. Ein wesentliches, neues Resultat ist eine Abschätzung der freien Energie nach oben durch die Energiedissipationsrate

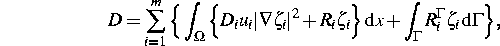
wie sie von uns in [4] unter gewissen Voraussetzungen an das Reaktionssystem, die für relevante Probleme aus der Halbleitertechnologie erfüllt sind, bewiesen worden ist. Derartige Abschätzungen für Reaktions-Diffusionssysteme mit ungeladenen Spezies gehen auf Gröger [7] zurück. In [3] erweitern wir die bisherigen Ergebnisse auf allgemeinere Statistiken, Stromrelationen und Reaktionsterme sowie auf eine nichtlineare Poisson-Gleichung.

Als Folgerung der Abschätzung der freien Energie durch die Energiedissipationsrate erhält man, daß die freie Energie entlang von Trajektorien des Systems exponentiell zu ihrem Gleichgewichtswert fällt, was die Stabilität des thermodynamischen Gleichgewichts bedeutet. Analoge Resultate sind auch für ein implizites Zeitdiskretisierungsschema nachgewiesen worden (siehe [4)].

Dabei sei betont, daß die bisherigen Aussagen ohne die Kenntnis von a priori-Schranken für Konzentrationen und Potentiale bewiesen werden. Im Gegenteil, wir verwenden diese Energieabschätzungen, um unter zusätzlichen Annahmen über die Positivität der Anfangswerte und über die Reaktionsordnung solche a priori-Abschätzungen zu gewinnen. Zunächst folgert man aus der globalen Beschränktheit der freien Energie mit Hilfe der Moser-Technik wie in [1] globale a priori-Abschätzungen für die Konzentrationen nach oben. Danach können wir, im Unterschied zu [1], aus dem exponentiellen Fallen der freien Energie schließen, daß die 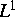-Norm von 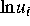, , 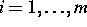global beschränkt ist. Durch Moser-Iteration kann damit die globale Beschränktheit der Konzentrationen nach unten durch eine positive, nur von den Daten des Problems abhängende Konstante gezeigt werden.

Um die Lösbarkeit der Aufgabe festzustellen, regularisieren wir das Problem durch ein ,,Abschneiden`` der Nichtlinearitäten in geeigneter Weise. Wir finden a priori-Abschätzungen für dieses regularisierte Problem, die nicht von dem Abschneidelevel abhängen, so daß Lösungen der regularisierten Aufgabe gleichzeitig Lösungen des Ausgangsproblems sind, wenn das Abschneidelevel hinreichend groß ist. Die Lösbarkeit der regularisierten Aufgabe wird über Zeitdiskretisierung und einen Auswahlsatz bewiesen. Wir erhalten die eindeutige Lösbarkeit unseres Problems, wobei für den Beweis der Einzigkeit 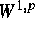-Regularitätsaussagen für elliptische Gleichungen von Gröger [6] verwendet werden. Diese Aussagen zur Existenz, Eindeutigkeit und zu globalen Abschätzungen von Lösungen der Aufgabe wurden in [5] zusammengestellt.

Projektliteratur:

1.   H. GAJEWSKI, K. GRÖGER, Reaction-diffusion processes of electrically charged species, WIAS-Preprint 118, Berlin, 1994.
2.   A. GLITZKY, K. GRÖGER, R. HÜNLICH, Discrete-time methods for equations modelling transport of foreign-atoms in semiconductors, erscheint in Nonlinear Analysis.
3.   , Free energy and dissipation rate for reaction diffusion processes of electrically charged species, eingereicht bei Applicable Analysis.
4.   A. GLITZKY, R. HÜNLICH, Energetic estimates and asymptotics for electro-reaction-diffusion systems, eingereicht bei Z. Angew. Math. Mech.
5.   , Electro-reaction-diffusion systems for heterostructures, eingereicht bei Proc. FBP'95.
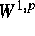6.   K. GRÖGER, A -estimate for solutions to mixed boundary value problems for second order elliptic differential equations, Math. Ann., 283 (1989), pp. 679--687.
7.   , Free energy estimates and asymptotic behaviour of reaction-diffusion processes, IAAS-Preprint 20, Berlin, 1992.
8.   , Boundedness and continuity of solutions to second order elliptic boundary value problems, Nonlinear Anal., 26 (1996), pp. 539--549.
9.   A. HÖFLER, N. STRECKER, On the coupled diffusion of dopants and silicon point defects, Technical Report 94/11, ETH Integrated Systems Laboratory, Zurich, 1994.
10.   N.S. TRUDINGER, On imbeddings into Orlicz spaces and some applications, J. of Mathematics and Mechanics, 17 (1967), pp. 473--483.