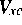Bearbeiter: H. Gajewski, H.-Chr. Kaiser, J. Rehberg, H. Stephan
Kooperation: H.-J. Wünsche, Institut für Physik, Humboldt-Universität zu Berlin;
P. Kleinert, Paul-Drude-Institut für Festkörperelektronik Berlin;
W. Heinrich, H. Wenzel, Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin
Förderung: BMBF-Förderprogramm ,,Anwendungsorientierte Verbundprojekte auf dem Gebiet der Mathematik``
Beschreibung der Forschungsarbeit:
Halbleiterlaser sind wegen ihrer Kompaktheit und Effizienz als Quelle kohärenter Strahlung weit verbreitet. Sie sind z. B. in jedem CD-Spieler als Abtastlaser (Emissionswellenlänge 780 nm) zu finden und spielen bei der Langstrecken-Nachrichtenübertragung über Glasfaserkabel als Sendelaser (Emissionswellenlängen 1300 und 1550 nm) eine entscheidende Rolle.
Gegenwärtig wird weltweit intensiv an der Verbesserung bestehender und der Entwicklung neuer Laserstrukturen gearbeitet. So versucht man, mit Halbleiterlasern immer kürzere Wellenlängen bis in den blauen Spektralbereich und immer höhere Ausgangsleistungen von mehr als einem Watt zu erzeugen. Vollkommen neue Strukturen stellen vertikal emittierende Laserdioden dar.
Ziel des Projektes ist die Unterstützung der Praxispartner bei der Entwicklung derartiger Bauelemente.
In Quantum-Well-Halbleiterlasern ist die aktive Schicht so dünn, daß Quanteneffekte berücksichtigt werden müssen. Zur Beschreibung solcher Effekte ist das Schrödinger-Poisson-System geeignet. Dieses System ist ein nichtlinear gekoppeltes System partieller Differentialgleichungen bestehend aus der Schrödingergleichung (Bestimmung der möglichen Zustände der Ladungsträger und deren Besetzungswahrscheinlichkeiten), der Poissongleichung (Bestimmung des von den Ladungsträgern erzeugten elektrischen Feldes) und Transportgleichungen (Berechnung der Umverteilung der Ladungsträger). Die analytischen und numerischen Untersuchungen zu diesem System wurden in diesem Jahr fortgesetzt.
Über die in [1] erzielten Resultate hinaus, gelang es in diesem Jahr, für
den physikalisch relevanten Fall mit Austausch-Korrelationspotential
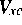folgendes zu beweisen (n ist die Elektronendichte):
Lemma 1. Die dem Austausch-Korrelations-Term der Schrödinger-Gleichung
entsprechende Abbildung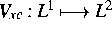 
bilde die Menge
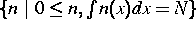in eine 
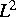-beschränkte Menge ab. Dann
hat das Schrödinger-Poisson-System eine Lösung.
Lemma 2. Bildet überdies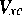 
die Menge 
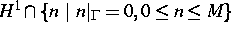für ein hinreichend großes, von den Daten des Problems
abhängiges M Lipschitz-stetig in 
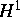ab und ist die Lipschitz-Konstante
dieser Abbildung hinlänglich klein, so ist die Lösung des
Schrödinger-Poisson-Systems sogar eindeutig bestimmt (z. B. im Fall kleiner
Kopplungskonstanten).
Des weiteren wurden verschiedene numerische Probleme untersucht. Unter anderem die Abhängigkeit der Eigenwerte und Eigenfunktionen des Schrödingeroperators von den Ansatzfunktionen und von der Wahl des Quantengebietes.
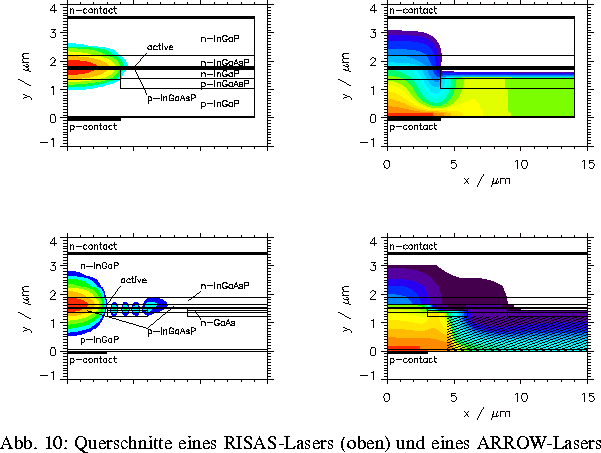
Mit dem von uns entwickelten 2D-Bauelementesimulator ToSCA wurden verschiedene praktisch relevante Hochleistungslaserdioden bezüglich eines minimalen Verluststromes optimiert. Die folgenden Bilder (aus [5]) zeigen die Simulation ausgewählter Strukturen (jeweils links die Intensität des optischen Feldes der Lasergrundmode und rechts das Quasiferminiveau der Löcher an der Laserschwelle).
Projektliteratur: