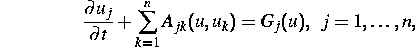




Bearbeiter: K. Gröger, J. Rehberg
Kooperation: M. Böhm, Humboldt-Universität zu Berlin
Beschreibung der Forschungsarbeit:
Es wurden Untersuchungen zur Existenz und Einzigkeit für Lösungen von quasilinearen parabolischen Systemen des Typs
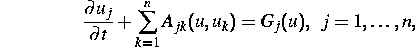
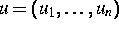 durchgeführt.
Die
durchgeführt.
Die 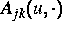 sind lineare Differentialoperatoren zweiter Ordnung mit
entsprechenden Randbedingungen, deren Koeffizienten wiederum von der Lösung
abhängen.
Die Operatoren
sind lineare Differentialoperatoren zweiter Ordnung mit
entsprechenden Randbedingungen, deren Koeffizienten wiederum von der Lösung
abhängen.
Die Operatoren 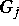 's sind den
's sind den 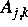 in gewissem Sinne untergeordnet und
können sehr unterschiedlicher Natur sein; u.a. sind die Driftstrom-Terme
sowohl der Halbleiter- wie der Chemotaxisgleichungen zugelassen.
Das Bestreben besteht nun gerade darin, für eine sehr große Klasse von
Gleichungen, darunter solche wie die Chemotaxis-Gleichungen, für die keine
a-priori-Energieabschätzungen existieren, eine möglichst allgemeine, lokale
Lösungstheorie bereitzustellen. Das Hauptproblem dabei ist, daß man
-- über
bekannte Ergebnisse hinaus -- mit Konstellationen konfrontiert ist, die sowohl
starke Nichtlinearitäten aufweisen als auch sehr ,,unglatt`` sind. Dies
betrifft
einerseits die Geometrie der Gebiete und die Tatsache, daß der Typ der
Randbedingung wechselt, wie auch die Eigenschaft der Koeffizienten, definitiv
unstetig zu sein. Das Konzept der Behandlung dieser Gleichungen besteht darin,
sie im Rahmen von
in gewissem Sinne untergeordnet und
können sehr unterschiedlicher Natur sein; u.a. sind die Driftstrom-Terme
sowohl der Halbleiter- wie der Chemotaxisgleichungen zugelassen.
Das Bestreben besteht nun gerade darin, für eine sehr große Klasse von
Gleichungen, darunter solche wie die Chemotaxis-Gleichungen, für die keine
a-priori-Energieabschätzungen existieren, eine möglichst allgemeine, lokale
Lösungstheorie bereitzustellen. Das Hauptproblem dabei ist, daß man
-- über
bekannte Ergebnisse hinaus -- mit Konstellationen konfrontiert ist, die sowohl
starke Nichtlinearitäten aufweisen als auch sehr ,,unglatt`` sind. Dies
betrifft
einerseits die Geometrie der Gebiete und die Tatsache, daß der Typ der
Randbedingung wechselt, wie auch die Eigenschaft der Koeffizienten, definitiv
unstetig zu sein. Das Konzept der Behandlung dieser Gleichungen besteht darin,
sie im Rahmen von 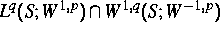 -Räumen anzuschauen
und zwar dergestalt in p und q, daß diese Räume stetige Einbettungen in
(raum-zeitliche) Hölder-Räume zulassen. Über einer Kugel in
-Räumen anzuschauen
und zwar dergestalt in p und q, daß diese Räume stetige Einbettungen in
(raum-zeitliche) Hölder-Räume zulassen. Über einer Kugel in
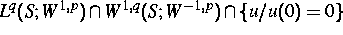 wird dann ein
geeignetes, kontraktives Iterationsschema definiert, das die zeitlich lokale
Existenz und Einzigkeit sichert.
Anzumerken ist noch, daß das hier verfolgte Vorgehen in voller Allgemeinheit
nur für die Raumdimension zwei funktioniert, im Falle höherer Raumdimension
müssen bestimmte Kleinheitsforderungen gestellt werden, die nicht stets
erfüllt sind.
wird dann ein
geeignetes, kontraktives Iterationsschema definiert, das die zeitlich lokale
Existenz und Einzigkeit sichert.
Anzumerken ist noch, daß das hier verfolgte Vorgehen in voller Allgemeinheit
nur für die Raumdimension zwei funktioniert, im Falle höherer Raumdimension
müssen bestimmte Kleinheitsforderungen gestellt werden, die nicht stets
erfüllt sind.
Projektliteratur:
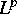 Regularity for Abstract Differential
Equations, LNM 1540 (1991), 25--38.
Regularity for Abstract Differential
Equations, LNM 1540 (1991), 25--38.
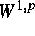 -estimate for solutions to mixed
boundary value problems for second order elliptic differential equations,
Math. Ann. 283 (1989), 679--687.
-estimate for solutions to mixed
boundary value problems for second order elliptic differential equations,
Math. Ann. 283 (1989), 679--687.
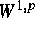 -estimates of solutions to
evolution equations corresponding to nonsmooth second order
elliptic differential operators, Nonlinear Analysis 18 (1992),
569--577.
-estimates of solutions to
evolution equations corresponding to nonsmooth second order
elliptic differential operators, Nonlinear Analysis 18 (1992),
569--577.
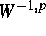 for second order elliptic differential operators in case of mixed boundary
conditions, Math. Ann. 285 (1989), 105--113.
for second order elliptic differential operators in case of mixed boundary
conditions, Math. Ann. 285 (1989), 105--113.



