



Bearbeiter: H. Schurz
Kooperation: S. Artemiev ( Novosibirsk), B. Mårtensson (Bremen)
Beschreibung der Forschungsarbeit:
Die automatisierte numerische Lösung stochastischer
dynamischer Systeme erfordert den Einsatz intelligenter und effizienter
Algorithmen zur Wahl geeigneter Schrittweiten und Konvergenzordnungen.
So braucht z.B. man dringend entsprechende Routinen zur Pfadverfolgung bzw.
zur Analyse von Phasendiagrammen. Bisher ist sehr wenig über die Gestalt
derartiger numerischer Integratoren für stochastische Modelle bekannt.
Erste numerische Experimente wurden an der Universität Bremen in Kooperation
mit Dr. B. Mårtensson bereits durchgeführt. Dabei zielen die Untersuchungen
auf eine pfadweise Fehlerkontrolle durch vorkonditionierte
stochastisch--numerische Verfahren. Schließlich wollen wir die Resultate in
das Simulationspaket
,,GNANS`` am Institut für Dynamische Systeme an der
Universität Bremen einbauen.
Eine Parallele dazu zeichnete sich in der Kooperation mit
einer Forschungsgruppe unter der Leitung von Prof. S.S. Artemiev am
Computerzentrum der Sibirischen Abteilung der Russischen Akadamie der
Wissenschaften in Novosibirsk
(Rußland) ab. Hierbei haben wir den Spezialfall additiven bzw. ,,kleinen``
Rauschens untersucht und einen Algorithmus mit variabler Schrittweite
entwickelt, der auf vorhandenen deterministischen Algorithmen basiert und am
Novosibirsker Computerzentrum auf eine im Programmsystem
,,DYNAMICS and CONTROL`` implementierbare Variante gebracht wurde. Eine entsprechende Dokumentation
ist als Preprint am WIAS (siehe [1]) erschienen. Als einen ersten Erfolg
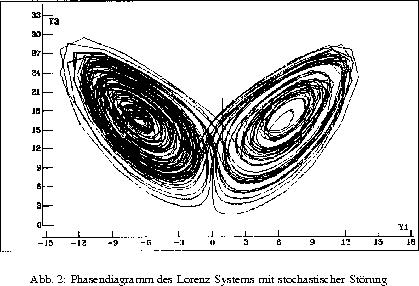
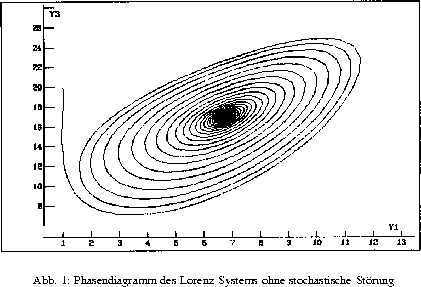
konnten wir darin Effekte stochastischer Störungen auf das Lorenz-, Rössler-
und Brusselator-System in der Phasenebene (vergleiche Bilder) zeigen.
Ein enger Zusammenhang besteht zu dem adaptiven Algorithmus für schwache
Approximationen, der in [2] entwickelt wurde.
Projektliteratur: