



Next: Adaptive Simulation stochastischer
Up: Projekte
Previous: Lokal adaptive Methoden
Bearbeiter: M. Nussbaum, V. Spokoiny
Beschreibung der Forschungsarbeit:
Grundlegende Aufgabenstellung ist die Approximation allgemeiner und
komplizierter
statistischer Modelle durch einfachere; es entsteht dabei eine Theorie, die
sich abstrakter Konzepte bedient und die (in der Tragweite für die
Statistik) etwa der Funktionalanalysis vergleichbar ist. Der Schwerpunkt der
Untersuchungen liegt bei den nichtparametrischen, d. h.
unendlichdimendionalen Problemen; eingeschlossen sind stochastische
inverse Probleme der Tomografie und Bildverarbeitung, Zusammenhänge zur
entsprechenden deterministischen Theorie sowie die Statistik stochastischer
Differentialgleichungen. Ein zentrales Thema in diesem Zusammenhang war die
asymptotische Äquivalenz nichtparametrischer Experimente zu Gaußschen
Folgen. Nachdem hier ein Durchbruch bei der Schätzung der
Wahrscheinlichkeitsdichte erzielt werden konnte (globale Gaußsche
Approximation für Modelle aus unabhängigen, identisch verteilten
Beobachtungen, s. [1]), gelang es nun, die Voraussetzungen auf ein kanonisches
Minimum zu reduzieren (Glattheit größer als 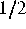 ). Entscheidend
hierfür war die Auswertung neuester Ergebnisse aus der Theorie der
empirischen Prozesse, speziell zu funktionalen KMT-Ungleichungen. Die
Anwendungsmöglichkeiten der asymptotischen Äquivalenz in der
nichtparametrischen Schätztheorie werden u. a. in [2] und [3] diskutiert.
). Entscheidend
hierfür war die Auswertung neuester Ergebnisse aus der Theorie der
empirischen Prozesse, speziell zu funktionalen KMT-Ungleichungen. Die
Anwendungsmöglichkeiten der asymptotischen Äquivalenz in der
nichtparametrischen Schätztheorie werden u. a. in [2] und [3] diskutiert.
Im Anschluß an die früheren Resultate zur Diskretisierung von
nichtparametrischen Diffusionsmodellen konnte gezeigt werden, daß für
ein Modell eines Martingal--Zählprozesses die Histogramm--Diskretisierung
ein statistisch äquivalentes Modell liefert. Weiterhin wurde die Grundlage
geschaffen für eine Diffusionsapproximation für Zählprozesse, in
Analogie zur white noise Approximation unabhängiger Beobachtungen. Diese
asymptotische Äquivalenz zu einem Diffusionsexperiment wurde zunächst
im parametrischen Fall gezeigt. Der nichtparametrische Fall beinhaltet
wesentliche Schwierigkeiten, die mit der Ausdehnung von KMT-Approximationen
auf Martingalmodelle zusammenhängen. Wahrscheinlichkeitstheoretische
Vorarbeiten hierzu (große Abweichungen für Martingale) finden sich in [4].
Die Überarbeitung der Monografie [5] für die englische Fassung bildete
einen weiteren Schwerpunkt; hierin werden wesentliche Beiträge zur
Methodik der Grenzexperimente dargestellt, die die klassischen Ergebnisse
von Le Cam auf nichtgaußsche Limites erweitern und den konstruktiven
Aspekt entwickeln . Zentral hierbei ist der Begriff der 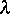 -Konvergenz,
der ein geignetes Limeskonzept für nichtgaußsche Grenzexperimente
bereitstellt (s. [6]). Diese Ergebnisse wurden auch in Form einer
Habilitationsschrift an der Humboldt-Universität vorgelegt.
-Konvergenz,
der ein geignetes Limeskonzept für nichtgaußsche Grenzexperimente
bereitstellt (s. [6]). Diese Ergebnisse wurden auch in Form einer
Habilitationsschrift an der Humboldt-Universität vorgelegt.
Projektliteratur:
- M. Nussbaum: Asymptotic equivalence of density estimation and white
noise. Erscheint in Ann. Statist.
- M. Nussbaum: Discussion on: ,,Wavelet Smoothing--Asymptopia ¿` by D.
Donoho, I. Johnstone, G. Kerkyacharian, D. Picard, (paper presented at the
session of the Royal Stat. Soc., Chapel Hill, NC, June 1994), erscheint in
J. Roy. Stat. Soc., Ser. B
- A. Korostelev, M. Nussbaum: Density estimation in the uniform norm
and white noise approximation. In Vorbereitung.
- I. Grama: On moderate deviations for martingales. WIAS Preprint
No. 121, Berlin (1994).
- A. Shiryaev, V. Spokoiny: Statistical Experiments and Decisions.
Asymptotic Theory. Verlag VINITI, Moskau, 1993, englische
Fassung erscheint bei Springer Verlag, New York. (Eingereicht als
Habilitationsschrift, Humboldt--Universität.)
- A. Shiryaev, V. Spokoiny, On the concept of
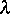 --convergence
of statistical experiments. Erscheint in: A. Novikov, A. Shiryaev, editors,
Statistics and Control for Stochastic Processes IV, Proceedings of the
Steklov Institute of Mathematics, 150, American Mathematical
Society, Providence.
--convergence
of statistical experiments. Erscheint in: A. Novikov, A. Shiryaev, editors,
Statistics and Control for Stochastic Processes IV, Proceedings of the
Steklov Institute of Mathematics, 150, American Mathematical
Society, Providence.




Next: Adaptive Simulation stochastischer
Up: Projekte
Previous: Lokal adaptive Methoden
BREMERO
Wed Apr 12 21:47:02 MDT 1995
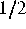 ). Entscheidend
hierfür war die Auswertung neuester Ergebnisse aus der Theorie der
empirischen Prozesse, speziell zu funktionalen KMT-Ungleichungen. Die
Anwendungsmöglichkeiten der asymptotischen Äquivalenz in der
nichtparametrischen Schätztheorie werden u. a. in [2] und [3] diskutiert.
). Entscheidend
hierfür war die Auswertung neuester Ergebnisse aus der Theorie der
empirischen Prozesse, speziell zu funktionalen KMT-Ungleichungen. Die
Anwendungsmöglichkeiten der asymptotischen Äquivalenz in der
nichtparametrischen Schätztheorie werden u. a. in [2] und [3] diskutiert.




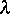 -Konvergenz,
der ein geignetes Limeskonzept für nichtgaußsche Grenzexperimente
bereitstellt (s. [6]). Diese Ergebnisse wurden auch in Form einer
Habilitationsschrift an der Humboldt-Universität vorgelegt.
-Konvergenz,
der ein geignetes Limeskonzept für nichtgaußsche Grenzexperimente
bereitstellt (s. [6]). Diese Ergebnisse wurden auch in Form einer
Habilitationsschrift an der Humboldt-Universität vorgelegt.
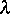 --convergence
of statistical experiments. Erscheint in: A. Novikov, A. Shiryaev, editors,
Statistics and Control for Stochastic Processes IV, Proceedings of the
Steklov Institute of Mathematics, 150, American Mathematical
Society, Providence.
--convergence
of statistical experiments. Erscheint in: A. Novikov, A. Shiryaev, editors,
Statistics and Control for Stochastic Processes IV, Proceedings of the
Steklov Institute of Mathematics, 150, American Mathematical
Society, Providence.