Konstruktive Methoden für Systeme stochastischer Differentialgleichungen mit farbigem und geringem Rauschen

Bearbeiter: G. Milstein

Beschreibung der Forschungsarbeit:

Bei der Realisierung von Methoden numerischer Integration von allgemeinen Systemen stochastischer Differentialgleichungen (SDE) entsteht eine Reihe von ernsthaften Problemen. Zum Beispiel benötigen Methoden mittlerer quadratischer Approximation ersten Genauigkeitsgrades die Modellierung vielfacher Ito-Integrale. Bei schwacher Approximation (solche Annäherung genügt für die Lösung von partiellen Differentialgleichungen mit Monte-Carlo-Methoden) gelingt es, das Problem der Modellierung komplizierter Zufallsgrößen zu vermeiden, jedoch entsteht hierbei das Problem der Konstruktion von Methoden des Runge-Kutta-Typs. Diese Methoden sind erforderlich, da in den Taylor-Typ-Methoden komplizierte Differentialoperatoren auftreten. Es gelingt, konstruktive Methoden für Systeme von speziellen Klassen zu finden. Hinreichend effiziente Methoden sowohl zur mitteren quadratischen als auch zur schwachen Approximation wurden für die Klasse von Systemen mit farbigem Rauschen in [1] entwickelt. Sie werden bei der Untersuchung physikalischer Vorgänge oft benutzt.

SDE mit geringem Rauschen sind eine andere wichtige Klasse von Systemen in der physikalischen Modellierung. Solche Systeme werden z. B. in vielen Untersuchungen benutzt, die mit stochastischer Resonanz zusammenhängen. Der neue Zugang zur numerischen Integration von SDE mit geringem Rauschen wird in [2], [3] dargelegt. Alle in [1]--[3] entwickelten Methoden sind praxisreif. Diese Methoden liegen zwischen deterministischen und stochastischen Methoden und sind dem Wesen der SDE mit geringem Rauschen adäquat. Sie wurden durch Berechnung der Lyapunov-Exponenten und durch Modellierung der stochastischen Resonanz getestet. Förderung: Deutscher Akademischer Austauschdienst (Partner M. Tret'yakov)

Projektliteratur:

1. G. Milstein, M. Tret'yakov: Numerical solution of differential equations with colored noise. J. Stat. Phys. 77, Nos. 3/4 (1994), pp. 691-715.
2. G. Milstein, M. Tret'yakov: Mean square approximation for stochastic differential equations with small noise. IAAS Preprint No. 102, Berlin (1994).
3. G. Milstein, M. Tret'yakov: Weak approximation for stochastic differential equations with small noise. WIAS Preprint No. 123, Berlin (1994).

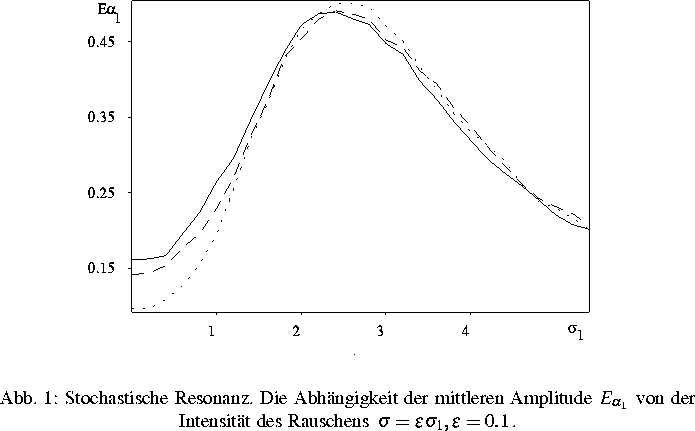
Schwache numerische Methoden für stochastische Differentialgleichungen mit kleinem Rauschen werden insbesondere zur Simulation der stochastischen Resonanz angewendet. Diese entsteht durch das Zusammenspiel zwischen kleinem Rauschen und periodischen Kräften in bistabilen Systemen.