



Next: Approximationstheorie stochastischer numerischer
Up: Projekte
Previous: Modellierung und numerische
Bearbeiter: N. Hofmann, H. Schurz
Beschreibung der Forschungsarbeit:
Zur Lösung stochastischer Differentialgleichungen (SDEs) sind zahlreiche
numerische Verfahren bekannt, vergleiche z.B. [1]. In [3] und [4] konnte die Entwicklung dieser Theorie durch eine
systematische Stabilitätsanalyse für numerische Lösungen fortgesetzt werden.
Zunächst wurden implizite Verfahren mit niedriger Konvergenzordnung bezüglich
der Testklasse linearer SDEs mit multiplikativem Rauschen im 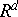 , die
wir als Linearisierung entsprechender nichtlinearer SDEs in einem stationären
Punkt interpretieren, untersucht. Wir analysierten das
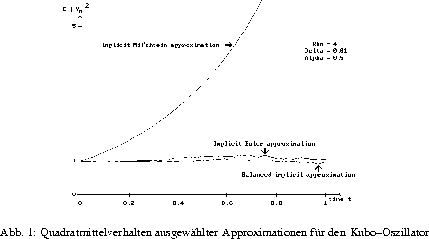
Quadratmittel--Stabilitätsverhalten der impliziten Milstein-Methoden und
der balancierten impliziten Methoden (zur Quadratmittelkonvergenz siehe [2])
bezüglich der Nullösung. Dabei erwies sich die Stabilität der
impliziten Euler-Methoden als eine notwendige Bedingung für die Stabilität
der impliziten Milstein-Methoden. Dies ist insofern bemerkenswert, als daß die
Milstein-Methoden eine höhere Ordnung der Quadratmittelkonvergenz als
die Euler-Methoden aufweisen. Desweiteren konnte eine hinreichende Bedingung
für die Quadratmittelstabilität der impliziten Euler-Methoden gefunden
werden. Außerdem ist die Korrektur mit stochastischen Termen in den
balancierten Methoden für deren Quadratmittelstabilität nicht notwendig.
Alle bisher genannten numerischen Methoden folgen dem Prinzip der
monotonen Inklusion der Quadratmittel-Stabilitätsbereiche. Die beschriebenen
Resultate reduzieren erheblich den Aufwand bei der Konstruktion
,,stochastisch-stabiler`` numerischer Verfahren, da eine stochastische Korrektur nun entfällt bei gleichzeitiger Wahrung der Stabilität der zweiten Momente.
, die
wir als Linearisierung entsprechender nichtlinearer SDEs in einem stationären
Punkt interpretieren, untersucht. Wir analysierten das
Quadratmittel--Stabilitätsverhalten der impliziten Milstein-Methoden und
der balancierten impliziten Methoden (zur Quadratmittelkonvergenz siehe [2])
bezüglich der Nullösung. Dabei erwies sich die Stabilität der
impliziten Euler-Methoden als eine notwendige Bedingung für die Stabilität
der impliziten Milstein-Methoden. Dies ist insofern bemerkenswert, als daß die
Milstein-Methoden eine höhere Ordnung der Quadratmittelkonvergenz als
die Euler-Methoden aufweisen. Desweiteren konnte eine hinreichende Bedingung
für die Quadratmittelstabilität der impliziten Euler-Methoden gefunden
werden. Außerdem ist die Korrektur mit stochastischen Termen in den
balancierten Methoden für deren Quadratmittelstabilität nicht notwendig.
Alle bisher genannten numerischen Methoden folgen dem Prinzip der
monotonen Inklusion der Quadratmittel-Stabilitätsbereiche. Die beschriebenen
Resultate reduzieren erheblich den Aufwand bei der Konstruktion
,,stochastisch-stabiler`` numerischer Verfahren, da eine stochastische Korrektur nun entfällt bei gleichzeitiger Wahrung der Stabilität der zweiten Momente.
Eine ähnliche Analyse konnte für die Klasse von linearen SDEs mit additivem
Rauschen durchgeführt werden. Allerdings sind stationäre Lösungen dieser SDEs
wieder Zufallsgrößen mit entsprechenden Charakteristika. Dadurch ergibt sich
eine größere Vielzahl von stochastischen Stabilitätskonzepten als in der
Deterministik. Es ist dann naheliegend, numerische Verfahren stärker im
Hinblick auf die Erhaltung stochastischer Charakteristika zu untersuchen.
Entsprechende Definitionen zur numerischen Erhaltung stationärer
Lösungen als auch eine erste Analyse der einfachsten Verfahren
bezüglich diesen Kriteriums sind in [4] zu finden.
Ausgehend von einer asymptotischen Entwicklung des globalen Fehlers für schwache
Taylor-Approximationen beliebiger Ordnung konnte ein Verfahren zur Ordnungs-und
Schrittweitensteuerung entwickelt werden, das sich auf Ideen von Deuflhard
bzgl. Anwendung der Extrapolationsmethode (siehe [5]) stützt.
Die theoretischen Grundlagen und die Beschreibung des resultierenden Algorithmus
bilden den Hauptteil der im September fertiggestellten Dissertation (siehe
[6]). Die Arbeit [6] enthält weiterhin einen Zugang zur systematischen Konstruktion von
schwachen Verfahren, die sich ausschließlich diskreter Zufallsvariablen
bedienen.
Projektliteratur:
- P.E. Kloeden, E. Platen, H.Schurz: Numerical solution
of stochastic differential equations through computer experiments,
Universitext, Springer, Berlin, 1994.
- G.N. Milstein, E. Platen, H. Schurz:
Balanced implicit methods for stiff stochastic systems,
Statistics Research Report No. SRR 029-94, Australian National
University, Canberra, 1994.
- H. Schurz: Asymptotical mean square stability of an
equilibrium point of some linear numerical solutions with multiplicative
noise, Preprint No. 108, WIAS, Berlin, 1994.
- H. Schurz: A note on pathwise approximation of stationary
Ornstein--Uhlenbeck processes with diagonalizable drift, Preprint No. 112,
WIAS, Berlin, 1994.
- P. Deuflhard: Order and stepsize control in extrapolation
methods, Num. Math. 41 (1983), pp.399-422.
- N. Hofmann: Beiträge zur schwachen Approximation stochastischer
Differentialgleichungen, Dissertation, Humboldt-Universität Berlin, 1994.




Next: Approximationstheorie stochastischer numerischer
Up: Projekte
Previous: Modellierung und numerische
BREMERO
Wed Apr 12 21:47:02 MDT 1995
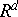 , die
wir als Linearisierung entsprechender nichtlinearer SDEs in einem stationären
Punkt interpretieren, untersucht. Wir analysierten das
Quadratmittel--Stabilitätsverhalten der impliziten Milstein-Methoden und
der balancierten impliziten Methoden (zur Quadratmittelkonvergenz siehe [2])
bezüglich der Nullösung. Dabei erwies sich die Stabilität der
impliziten Euler-Methoden als eine notwendige Bedingung für die Stabilität
der impliziten Milstein-Methoden. Dies ist insofern bemerkenswert, als daß die
Milstein-Methoden eine höhere Ordnung der Quadratmittelkonvergenz als
die Euler-Methoden aufweisen. Desweiteren konnte eine hinreichende Bedingung
für die Quadratmittelstabilität der impliziten Euler-Methoden gefunden
werden. Außerdem ist die Korrektur mit stochastischen Termen in den
balancierten Methoden für deren Quadratmittelstabilität nicht notwendig.
Alle bisher genannten numerischen Methoden folgen dem Prinzip der
monotonen Inklusion der Quadratmittel-Stabilitätsbereiche. Die beschriebenen
Resultate reduzieren erheblich den Aufwand bei der Konstruktion
,,stochastisch-stabiler`` numerischer Verfahren, da eine stochastische Korrektur nun entfällt bei gleichzeitiger Wahrung der Stabilität der zweiten Momente.
, die
wir als Linearisierung entsprechender nichtlinearer SDEs in einem stationären
Punkt interpretieren, untersucht. Wir analysierten das
Quadratmittel--Stabilitätsverhalten der impliziten Milstein-Methoden und
der balancierten impliziten Methoden (zur Quadratmittelkonvergenz siehe [2])
bezüglich der Nullösung. Dabei erwies sich die Stabilität der
impliziten Euler-Methoden als eine notwendige Bedingung für die Stabilität
der impliziten Milstein-Methoden. Dies ist insofern bemerkenswert, als daß die
Milstein-Methoden eine höhere Ordnung der Quadratmittelkonvergenz als
die Euler-Methoden aufweisen. Desweiteren konnte eine hinreichende Bedingung
für die Quadratmittelstabilität der impliziten Euler-Methoden gefunden
werden. Außerdem ist die Korrektur mit stochastischen Termen in den
balancierten Methoden für deren Quadratmittelstabilität nicht notwendig.
Alle bisher genannten numerischen Methoden folgen dem Prinzip der
monotonen Inklusion der Quadratmittel-Stabilitätsbereiche. Die beschriebenen
Resultate reduzieren erheblich den Aufwand bei der Konstruktion
,,stochastisch-stabiler`` numerischer Verfahren, da eine stochastische Korrektur nun entfällt bei gleichzeitiger Wahrung der Stabilität der zweiten Momente.




