



Next: Dünne organische Schichten
Up: Projekte
Previous: Verzweigungsprozesse in katalytischen
Bearbeiter: K. Fleischmann
Kooperation: J.T. Cox (Syracuse), A. Greven (Erlangen)
Beschreibung der Forschungsarbeit:
Die Herausbildung zufälliger Cluster kann in vielen angewandten
Gebieten beobachtet werden (z.B. Rostbildung an glatten Stahlflächen,
Sonnenflecke, Akkumulationseffekte, Keimbildung). Sie ist von
grundsätzlich anderer Natur als häufig anzutreffende
Mittelungsprinzipien. Von besonderem Interesse ist die sogenannte
diffusive Clusterbildung: Charakteristika der Cluster (wie Größe oder
Form) bleiben selbst in makroskopischen Skalen zufällig.
Wechselwirkende Diffusionen stammen vor allem aus der
Populationskinetik. Sie beschreiben in der Diffusionsapproximation
Häufigkeiten des Auftretens von Genen unter dem Einfluß von Resampling
und Migration. In der kritischen Dimension besitzen solche Prozesse gerade
die diffusive Clusterbildungseigenschaft [1]. Sie ist darüber hinaus
universell: Die
Limesstrukturen sind für eine große Klasse von Diffusionskoeffizienten and
Anfangsszuständen identisch.
Im Berichtsjahr wurde ein allgemeines Vergleichsargument bewiesen
([2]). Es ermöglicht, ein seit Jahren angestrebtes Resultat zu
erzielen: Vorausgesetzt der Träger des Diffusionskoeffizienten ist die
Halbachse und die Migrationsirrfahrt ist rekurrent, dann stirbt die
unendliche wechselwirkende Diffusion lokal.
Gebraucht wird diese Vergleichsmethode auch für das Studium der
zeitlichen Struktur der Clusterformierung für wechselwirkende Diffusionen
im Intervall 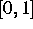 (s. [3]). Ein zu einem späten Zeitpunkt
vorliegender Cluster hat auch makroskopisch ein zufälliges Alter. Dies ist
von kleinerer Ordnung als das Systemalter. Weiter zurückliegende Cluster
indes haben eine asymptotisch verschwindende Lebenszeit: Ihre Zustände
bilden ein bedingtes 0-1-Rauschen. Der sogenannte transformierte
Fischer--Wright--Baum ist ein
wesentliches Hilfsmittel zur
Beschreibung der genealogischen Struktur der Raum-Zeit-Cluster.
Er ist in
Dualität zu einem Ensemble von Log-Verschmelzern, das als Limesstruktur zu
verzögerten verschmelzenden Irrfahrten mit Immigrationen auftritt. Diese
sind wiederum in Dualität zu wechselwirkenden Fisher-Wright-Diffusionen.
(s. [3]). Ein zu einem späten Zeitpunkt
vorliegender Cluster hat auch makroskopisch ein zufälliges Alter. Dies ist
von kleinerer Ordnung als das Systemalter. Weiter zurückliegende Cluster
indes haben eine asymptotisch verschwindende Lebenszeit: Ihre Zustände
bilden ein bedingtes 0-1-Rauschen. Der sogenannte transformierte
Fischer--Wright--Baum ist ein
wesentliches Hilfsmittel zur
Beschreibung der genealogischen Struktur der Raum-Zeit-Cluster.
Er ist in
Dualität zu einem Ensemble von Log-Verschmelzern, das als Limesstruktur zu
verzögerten verschmelzenden Irrfahrten mit Immigrationen auftritt. Diese
sind wiederum in Dualität zu wechselwirkenden Fisher-Wright-Diffusionen.
Projektliteratur:
-
K. Fleischmann, A. Greven: Diffusive clustering
in an infinite system of hierarchically interacting diffusions.
Probab. Theor. Relat. Fields, 98, 517--566 (1994)
-
J.T. Cox, K. Fleischmann, A. Greven:
Comparison of interacting diffusions and application to their ergodic
theory.
WIAS--Preprint Nr. 135 (1994), eingereicht bei: Probab. Theor. Relat. Fields
-
K. Fleischmann, A. Greven: Time-space analysis
of the cluster-formation in interacting diffusions
WIAS--Preprint Nr. 122 (1994), eingereicht bei: Stochastic Process. Appl.




Next: Dünne organische Schichten
Up: Projekte
Previous: Verzweigungsprozesse in katalytischen
BREMERO
Wed Apr 12 21:47:02 MDT 1995
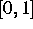 (s. [3]). Ein zu einem späten Zeitpunkt
vorliegender Cluster hat auch makroskopisch ein zufälliges Alter. Dies ist
von kleinerer Ordnung als das Systemalter. Weiter zurückliegende Cluster
indes haben eine asymptotisch verschwindende Lebenszeit: Ihre Zustände
bilden ein bedingtes 0-1-Rauschen. Der sogenannte transformierte
Fischer--Wright--Baum ist ein
wesentliches Hilfsmittel zur
Beschreibung der genealogischen Struktur der Raum-Zeit-Cluster.
Er ist in
Dualität zu einem Ensemble von Log-Verschmelzern, das als Limesstruktur zu
verzögerten verschmelzenden Irrfahrten mit Immigrationen auftritt. Diese
sind wiederum in Dualität zu wechselwirkenden Fisher-Wright-Diffusionen.
(s. [3]). Ein zu einem späten Zeitpunkt
vorliegender Cluster hat auch makroskopisch ein zufälliges Alter. Dies ist
von kleinerer Ordnung als das Systemalter. Weiter zurückliegende Cluster
indes haben eine asymptotisch verschwindende Lebenszeit: Ihre Zustände
bilden ein bedingtes 0-1-Rauschen. Der sogenannte transformierte
Fischer--Wright--Baum ist ein
wesentliches Hilfsmittel zur
Beschreibung der genealogischen Struktur der Raum-Zeit-Cluster.
Er ist in
Dualität zu einem Ensemble von Log-Verschmelzern, das als Limesstruktur zu
verzögerten verschmelzenden Irrfahrten mit Immigrationen auftritt. Diese
sind wiederum in Dualität zu wechselwirkenden Fisher-Wright-Diffusionen.



