



Bearbeiter: S. Hengst
Kooperation: C. J. van Duijn (TU Delft), P. Knabner (Universität Erlangen--Nürnberg)
Beschreibung der Forschungsarbeit:
Gegenstand der Untersuchung sind chemisch bedingte
Transportprozesse in porösen Medien mit an einer Auflösungsreaktion
beteiligten Komponenten. Es
wird eine rasch verlaufende ,,klassische`` Reaktion
betrachtet, wobei die
Reaktionsraten ausschließlich durch die chemische
Kinetik
(zeitlicher Ablauf der Reaktion) bestimmt sind. Im
Gegensatz zu anderen
möglichen Zugängen schließt das betrachtete
Modell auch die
Gleichgewichtssituation mit ein. Die mathematische
Formulierung des Problems
führt auf zwei Diffusions--Konvektionsgleichungen für
die Anionen-- und
Kationenkonzentrationen und eine gewöhnliche
Differentialgleichung, die die
eingehenden Auflösungsreaktionen beschreibt. Die
Hauptschwierigkeit liegt
in der Mengenwertigkeit der Nichtlinearität
(Heaviside--Graph) in der
Reaktionsgleichung, die scharfe Auflösungsfronten der
Lösungen
gestattet.
Die numerische Lösung des Randwertproblems erfolgt
mit
einem Schießalgorithmus und gestattet die
Untersuchung aller qualitativer
Eigenschaften der Lösung in Form laufender Wellen mit
scharfer
Auflösungsfront einschließlich dem Nachweis der
Konvergenzraten
beim Übergang zur Gleichgewichtsreaktion und für
verschwindende
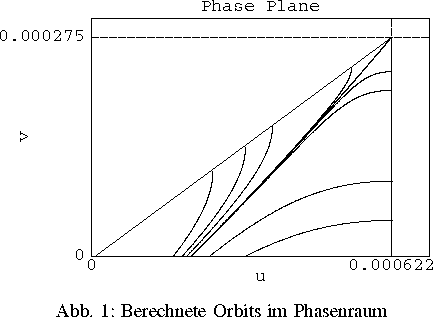
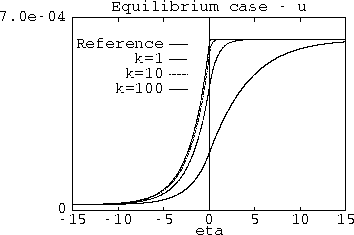
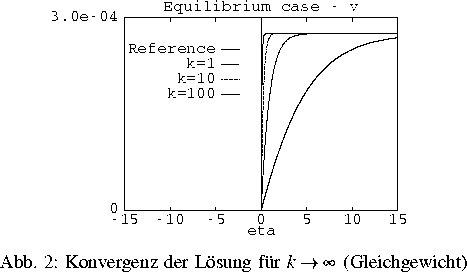
Dispersion. Die numerischen Resultate bestätigen die theoretischen
Aussagen in vollem Umfang (siehe Abb. 1 und 2).
Für die Entwicklung leistungsfähiger
Mehrphasenmodelle zur Simulation von
Ausbreitungsvorgängen bei Schadstoffen aber auch beim
Problem der optimalen
Ausbeute von Lagerstätten spielt die
Modellierung eine entscheidende
Rolle. Entsprechende Resultate für Zweiphasenströmungen im
zweidimensionalen Fall finden sich in der Literatur.
Motiviert durch erste Testrechnungen für eine
Zweiphasenströmung in 3D (siehe Projekt ,,Gesättigt--ungesättigter
Fluidtransport in porösen Medien``) wird für die
Strömung zweier inkompressibler Flüssigkeiten (Wasser, Öl) in der
Druck--Sättigungsformulierung
in 3 Raumdimensionen die Frage nach Existenz und
Eindeutigkeit der
Lösung gestellt. Erste theoretische Ergebnisse dazu
sind erfolgversprechend,
werden jedoch erst 1995 veröffentlicht.
Projektliteratur:






