Bearbeiter: G. Hebermehl, R. Schlundt
Kooperation: W. Heinrich, J. Gerdes, H. Zscheile (Ferdinand--Braun--Institut für Höchstfrequenztechnik (FHB)
Beschreibung der Forschungsarbeit:
Der Entwurf monolithisch integrierter Mikrowellenschaltungstechnik
(MMIC) erfordert die Entwicklung und Nutzung zuverlässiger
Simulationswerkzeuge, um zeit-- und kostenaufwendige technologische
Entwicklungszyklen zu vermeiden. Der Einsatz von Schaltungen im
GHz--Bereich (1 -- 100 GHz) erfolgt u.a. in mobilen Kommunikationssystemen.
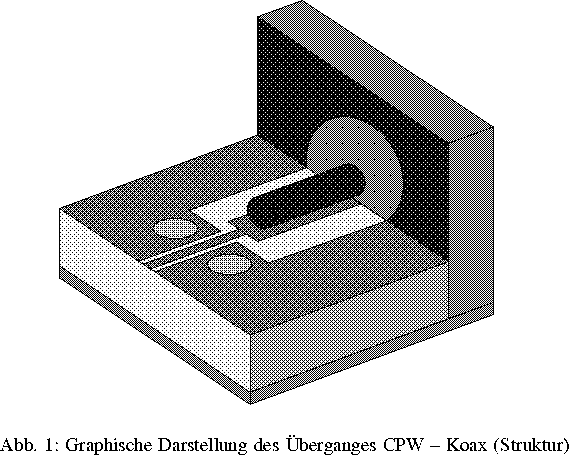
Die Entwicklung geeigneter Ersatzschaltbilder für den Schaltungsentwurf
erfolgt im FBH rechnergestützt durch elektromagnetische Feldsimulation.
Innerhalb eines dreidimensionalen Gebietes sind die Maxwellschen
Gleichungen (Randwertproblem) zu lösen. Als elektrische Zuführung
für dieses Gebiet werden
längshomogene Wellenleiter verwendet, deren Beschreibung mit Hilfe
eines Exponentialansatzes auf ein zweidimensionales Problem reduziert
wird.
Die aufwendigen Teile der Simulation bestehen in der Bestimmung von
Eigenwerten und --vektoren für ein zweidimensionales Gebiet und in der
Lösung von Gleichungssystemen in einem dreidimensionalen Raum. Die
Ergebnisse bestehen letztendlich aus einigen Zahlen (Streumatrix), die
dem Elektrotechniker als charakteristische Größen von
Ersatzschaltbildern dienen und eine Basis für den Entwurf von
Schaltungen bilden.
Für die Simulation werden am FBH Tools verwendet, die auf einer
Finite--Volumen--Methode (in der Ingenieursprache FDFD,
Finite--Difference Method in Frequency Domain) basieren und auf
Programmen aufbauen, die an der TH Darmstadt entwickelt wurden.
Die Lösung eines Problems mit diesen Tools auf einer
modernen Alpha--Workstation kann für die Eigenwertaufgabe Tage und für
die Gleichungssysteme bis zu einer Woche in Anspruch nehmen.
Das sind unakzeptable Antwortzeiten, wenn noch berücksichtigt wird,
daß für jede Rechnung ein umfangreicher Ausgangsdatensatz fehlerfrei
bereitgestellt werden muß. Außerdem besteht der Wunsch, kompliziertere
Schaltungen zu berechnen und zur Erreichung höherer Genauigkeiten mit
feinerer Diskretisierung zu arbeiten, so daß Eigenwertprobleme und
Gleichungssysteme höherer Ordnung (bisher maximal 7000 Gleichungen
für das Eigenwertproblem und ca. 
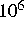Gleichungen für das lineare
Gleichungssystem) zu behandeln sind. Neben dem Rechenzeitbedarf steht
Rechnungen mit höheren Dimensionen vor allem der begrenzte Speicherplatz
(Alpha--Workstation, 512 MByte) im Wege. Langfristig soll das Problem
durch Parallelisierung in Kombination mit adaptiven Multilevel--Verfahren
gelöst werden.
Um kurzfristig Abhilfe zu schaffen, wurde zunächst an einer Verbesserung
der rechenintensiven Teile des Verfahrens für Workstations gearbeitet.
(1) Eigenwertproblem
Es handelt sich um ein Eigenwertproblem mit nichtsymmetrischer, schwach
besetzter Matrix, die in der ursprünglichen Programm--Version
als voll besetzte Matrix abgespeichert ist. Es
werden alle Eigenwerte berechnet und aus diesen ausgewählte zugehörige
Ausbreitungskonstanten bestimmt.
Für die
zunächst interessierenden reellen Ausbreitungskonstanten wurde ein Weg
gefunden, der es gestattet, die gewünschte Untermenge von
Ausbreitungskonstanten mit dem Arnoldi--Verfahren zu berechnen. Die
Rechenzeit konnte dadurch um den Faktor 30 gesenkt werden.
Die Berechnung der Eigenwerte und --vektoren gelingt für das vorliegende
Eigenwertproblem nur im 'invert mode', d.h., in jedem Iterationsschritt
ist ein lineares Gleichungssystem (LU-Dekomposition zu Beginn der
Iteration, Vorwärts-- und Rückwärtseinsetzen in jedem Iterationsschritt) zu lösen.
Durch den Übergang zur Sparse--Matrix--Technik im direkten Verfahren
zur Lösung linearer Gleichungssysteme konnte eine wesentliche
Speicherplatzreduzierung erreicht werden, so daß am FBH jetzt Aufgaben
höherer Dimension gerechnet werden können.
Weiter wurde eine Verbesserung der Genauigkeit erreicht.
(2) Lineares Gleichungssystem
Die Koeffizientenmatrix des linearen Gleichungssystems ist reell und
symmetrisch. Die positive Definitheit kann nicht vorausgesetzt werden.
In dem Darmstädter Programm wird zur Lösung der linearen
Gleichungssysteme das klassische CG--Verfahren in ,,veralteter``
Schreibweise verwendet.
Zur Lösung der großdimensionalen linearen Gleichungssysteme mit
reellen und symmetrischen Koeffizientenmatrizen erwiesen sich das
symmetrische LQ--Verfahren (SYMMLQ) und die symmetrische QMR--Methode
ohne look--ahead in der BCG--Variante (QMR--from--BCG) als brauchbare
Algorithmen.
Ausgehend von der Skalierung wird die symmetrische SOR--Vorkonditionierung
(SSOR) benutzt.
Zusätzlich wurden durch Untersuchungen die Dimension der Gleichungssysteme reduziert und eine angepaßtere Speicherungsform verwendet.
Es konnte eine Reduzierung der Rechenzeit um ca. 50--70% erzielt werden.
