



Bearbeiter: R. Kornhuber, H. Langmach
Kooperation: R. H. W. Hoppe (TU München), H. Yserentant (Universität Tübingen), R. Beck, B. Erdmann, R. Roitzsch (ZIB Berlin)
Beschreibung der Forschungsarbeit:
Das Projekt ist die Fortsetzung eines entsprechenden Vorhabens am Konrad-Zuse-Zentrum Berlin (ZIB).
Die Entwicklung von monotonen Mehrgittermethoden bedeutete einen Durchbruch bei der schnellen Lösung von Hindernisproblemen (siehe Jahresbericht 1993 des ZIB). Die Grundidee besteht in der Erweiterung des klassischen nichtlinearen Gauß--Seidel--Verfahrens durch zusätzliche Grobgitterkorrekturen, die sich aus der Optimierung des Energiefunktionals in zusätzliche ,,niederfrequente`` Suchrichtungen ergeben. Da die direkte Anwendung des so entstandenen Iterationsverfahrens zu aufwendig ist, ersetzt man die entsprechenden Grobgitterprobleme durch quasioptimale Approximationen. Diese Approximationen sind in lokal exakt und erhalten zusammen mit der Monotonie auch die globale Konvergenz des ursprünglichen Verfahrens, ermöglichen aber auf der anderen Seite die effiziente Implementierung als V--Zyklus. Eine zusätzliche Anpassung (Abschneiden) der Suchrichtungen am freien Rand führt darüberhinaus zu drastischen Verbesserungen der Konvergenzgeschwindigkeit. Durch Verfeinerung der linearen Theorie erhält man logarithmische a priori Schranken für die asymptotischen Konvergenzraten. Wie schon früher angedeutet, läßt sich diese Vorgehensweise grundsätzlich auf alle diskreten Optimierungsprobleme übertragen, für die das (nichtlineare) Gauß--Seidel--Verfahren konvergiert.
Im Berichtsjahr wurden konvexe, stückweise quadratische Optimierungsprobleme betrachtet, wie sie etwa bei der impliziten Zeitdiskretisierung von Stefan--Problemen in Enthalpie--Formulierung entstehen. In diesem Fall führt man die quasioptimale Approximation der Grobgitterprobleme durch die Forderung nach Invarianz des aktuellen freien Randes unter der Grobgitterkorrektur auf entsprechende Resultate für Hindernisprobleme zurück. Das aktuelle Hindernis wird zusammen mit dem aktuellen freien Rand durch die Feingitterglättung eingestellt. Die resultierenden monotonen Mehrgittermethoden sind nach wie vor global konvergent und es gelten dieselben Abschätzungen der asymptotischen Konvergenzraten wie für Hindernisprobleme. Auch die numerischen Ergebnisse sind vergleichbar [1].
Im Unterschied zu bisher bekannten Mehrgittermethoden für Stefan-artige Probleme erlaubt unser neuer Zugang die Kopplung der unterschiedlichen Phasen über die Grobgitterkorrektur. So erhält man nicht nur bessere Konvergenzraten sondern auch ein robustes Verhalten gegenüber der Anzahl der Phasen. Diese Eigenschaft motiviert die stückweise lineare Approximation stückweise glatter Enthalpiefunktionen, wie sie zum Beispiel bei der Poröse--Medien--Gleichung auftreten. Auf diese Weise lassen sich einerseits wesentliche Eigenschaften des kontinuierlichen Problems bei der Diskretisierung erhalten und andererseits die resultierenden diskreten Probleme schnell lösen [2].
Adaptive Techniken zur Konstruktion einer geeigneten Hierarchie von Gittern basieren wesentlich auf zuverlässigen a posteriori Schätzungen des Diskretisierungsfehlers. Zu diesem Zweck wurden hierarchische Fehlerschätzer für Variationsungleichungen entwickelt und analysiert [2]. Insbesondere erhält man eine Einschließ ung des Diskretisierungsfehlers, bei der die auftretenden Konstanten von einer Saturationsbedingung, einer Genauigkeitsbedingung an die iterative Lösung und vom Verhalten des diskreten freien Randes abhängen.
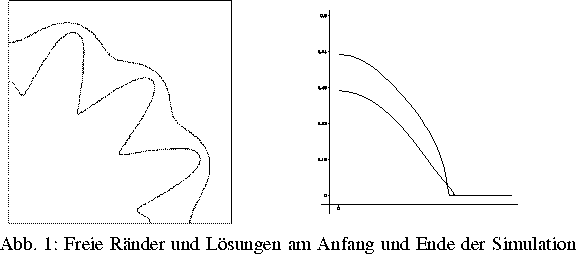
Die Abbildungen 1 und 2 illustrieren die approximative Lösung der Poröse-Medien-Gleichung für eine Anfangsbedingung mit fingerförmigem, kompaktem Träger [2]. Das linke Bild in Abbildung 1 zeigt den freien Rand nach dem ersten und dem vierzigsten Zeitschritt, während das rechte Bild die zugehörigen Approximationen entlang eines diagonalen Schnittes darstellt. Wie oben angedeutet ist dabei die als Enthalpie auftretende Wurzelfunktion unter Erhaltung der endlichen Ausbreitungsgeschwindigkeit stückweise linear approximiert worden. Abbildung 2 zeigt die entsprechenden adaptiv erzeugten Gitter.


Projektliteratur:



