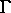Bearbeiter: W. Müller, K.R. Schneider
Kooperation: A. Shoshitaishvili (Institut für Steuerungsprobleme der Russischen Akademie der Wissenschaften, Moskau)
Beschreibung der Forschungsarbeit:
Es wurden Fragen der
Konstruktion von Beobachtern für Systeme untersucht, bei denen sowohl das
beschreibende Differentialgleichungssystem als auch die einer Messung
zugänglichen Output--Größen invariant bezüglich einer (endlichen oder
diskreten) Gruppe 
von Transformationen sind.
Es geht dann um die Beobachtung (d.h. Approximation) einer Menge
von (allein durch die Auswertung der Output--Größen nicht unterscheidbaren)
Zustandspunkten, die aus einem oder mehreren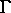 
--Orbits besteht.
Es konnte gezeigt werden, daß in derartigen Situationen die Konstruktion eines
Beobachters mit Hilfe eines üblichen einwertigen Output--Feedback vom Prinzip
her nicht möglich ist, daß aber unter relativ allgemeinen Voraussetzungen
mittels verzweigter (d.h. mehrwertiger)
und erforderlichenfalls dynamischer Output--Feedbacks brauchbare
Beobachter konstruiert werden können.
Das vorgeschlagene Konstruktionsverfahren basiert auf der
Verwendung der Ashby--Relation, die
bereits bei anderen Aufgabenstellungen zur Gewinnung stabilisierender
Feedback-Steuerungen benutzt wurde. Es liefert
zusätzlich zu der verzweigten Feedback--Steuerfunktion eine Vorschrift,
die angibt, in welcher Weise und zu welchen Zeitpunkten die Steuerung von
einem Zweig der Feedback--Steuerfunktion zu einem anderen Zweig springt.
Hierzu benötigte Hilfsgrößen können ihrerseits mit Hilfe eines
Beobachters vom Luenberger--Typ asymptotisch approximiert werden, dadurch
kann die explizite Verwendung von zeitlichen Ableitungen des System--Outputs
im Konstruktionsprozeß umgangen werden.
Als ein mögliches Anwendungsbeispiel
wurde die Stabilisierung der Rotationsbewegung eines starren Körpers
betrachtet.
Einige Ergebnisse werden in [1] dargestellt.
Förderung: DFG, Gästemittel
Projektliteratur: