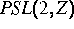Bearbeiter: A. Juhl
Kooperation: U. Bunke, M. Olbrich (Humboldt--Universität zu Berlin, SFB 288), A. Deitmar (Universität Heidelberg, z.Zt. Berkeley (USA)), D. Mayer (Universität Clausthal--Zellerfeld), S. Patterson, V. Schubert (Universität Göttingen), R. Sulanke (Humboldt--Universität zu Berlin)
Beschreibung der Forschungsarbeit:
Hauptobjekt der Untersuchungen ist die Dynamik des geodätischen Flusses von Mannigfaltigkeiten mit einer Riemannschen Metrik negativer Krümmung. Der geodätische Fluß einer solchen Metrik ist sowohl ein Hamiltonsches dynamisches System als auch ein hyperbolisches System im Sinne der Dynamik. Vom Standpunkt der mathematischen Physik aus hat man es hier mit der Untersuchung einer Dynamik mit starkem Chaos (im Sinne von Gutzwiller) zu tun.
Die Zeta-Funktionen haben sich als das wichtigste mathematische Objekt erwiesen, in dem die Verbindung zwischen der Struktur der periodischen Bahnen und den globalen Eigenschaften der Dynamik (Entropie, BSR-Ma etc.) gespeichert sind. Ist nun die Dynamik reell-analytisch und sind auch die stabilen und unstabilen Blätterungen reell-analytisch, so ist nach grundlegenden Sätzen von Ruelle und Fried die Zeta-Funktion meromorph. Ihre Nullstellen und Polstellen (Singularitäten) werden durch das Spektrum von Perron-Frobenius-Operatoren (Ruelle-Operatoren) vollständig beschrieben. Die tieferliegenden Eigenschaften dieser Spektren sind aber bisher bereits in den einfachsten Spezialfällen kaum verstanden.
Auf der anderen Seite verfügt man durch die Methoden der harmonischen Analysis (etwa der Lorentz-Gruppe) über starke Hilfsmittel zur Untersuchung der gleichen Zeta-Funktionen. Viele der auf diesem Wege ableitbaren Ergebnisse sind bisher aber vom Standpunkt der Dynamik aus noch nicht reproduzierbar. In der Tat hat man es hier mit einer gro Lücke in unserem gegenwärtigen Verständnis dieser Dynamiken zu tun. Die Erhellung dieser Zusammenhänge ist insbesondere auch für die numerischen Untersuchungen der Spektren der entsprechenden Perron-Frobenius-Operatoren, wie sie etwa in der mathematischen Physik des Quantenchaos durchgeführt werden, von Bedeutung.
Diese Situation war Anlaß, nach einer vollständigen Beschreibung der Singularitäten der Zeta-Funktionen durch Invarianten der unterliegenden Dynamik zu suchen. Im Gegensatz zu einer solchen Beschreibung liefern die Methoden der harmonischen Analysis eine völlig andersartige Charakterisierung der Singularitäten. Es gelang hier, die Verhältnisse insbesondere für die geodätischen Flüsse kompakter Räume konstanter negativer Krümmung ganz aufzuklären. Der grundlegende Ansatz besteht darin, die Perron-Frobenius-Operatoren nur als eine Approximation der Wahrheit zu betrachten, die in der induzierten Dynamik auf Räumen von Differentialformen mit distributiven Koeffizienten ( kanonische Ströme) liegt, d.h., es wurden Eigenfunktionen von Perron-Frobenius-Operatoren durch kanonische Ströme ersetzt. Die Definition der Elemente dieser Räume ist eine natürliche Verallgemeinerung des Begriffes des invarianten Ma. Insbesondere liefert das Sinaï-Bowen-Ruelle-Maß ein Element der eingeführten Räume kanonischer Ströme. Diese Ströme sind auch ohne ihren Zusammenhang zu den Zeta-Funktionen von Interesse. Insbesondere sind sie für viele andere Attraktoren interessant. Eine hervorragende Rolle spielen hierbei die Limes-Mengen gebrochen-rationaler Abbildungen der Sphäre.
Die skizzierten Ergebnisse haben verschieden Wurzeln in vorangegangenen Untersuchungen und Vermutungen zu einer kohomologischen Theorie der Zeta-Funktionen hyperbolischer dynamischer Systeme, wie sie seit einigen Jahren in diesem Projekt und unabhängig davon durch S. Patterson (Göttingen) angeregt und durchgeführt wurden. Die Ergebnisse der o.g. Untersuchungen sind in verschiedener Hinsicht überraschend. So ist es nicht von vornherein sicher, daß man überhaupt dynamische Invarianten findet, die für die angestrebte Charakterisierung der Singularitäten der Zeta-Funktionen brauchbar sind. Es gab in der Literatur kein Vorbild für die hier entwickelte Theorie.
Weiterhin weist die hier entwickelte Definition der kanonischen Ströme auf prinzipielle Auswirkungen der Hamiltonschen Struktur der Systeme auf die Spektren der Perron-Frobenius-Operatoren hin, die bisher nicht beachtet und untersucht wurden.
In unmittelbarer Verbindung zu der oben beschriebenen Theorie wurden Untersuchungen des geodätischen Flusses der Modulfläche durchgeführt. Dies ist ein Beispiel einer hyperbolischen Dynamik auf einer nicht-kompakten Mannigfaltigkeit mit einer Spitze. Hierbei spielen die ins Unendliche (Spitze) laufenden Bahnen eine wichtige Rolle für das Verständnis der Zeta-Funktionen. Vom Standpunkt der Perron-Frobenius-Operatoren ist dies der bisher einzige Spezialfall eines hyperbolischen geodätischen Flusses, für den man die Spektren dieser Operatoren genauer untersuchen kann. In den vergangenen Jahren wurden in dieser Richtung eine Vielzahl sehr erstaunlicher Entdeckungen gemacht (D. Mayer, J. Lewis, I. Efrat, D. Zagier u.v.a.), die jetzt zu einer raschen Entwicklung auf diesem Gebiet geführt haben. So werfen diese Untersuchungen z.B. neues Licht auf klassische Probleme in der Theorie der Modulformen. Es zeigt sich, daß der Standpunkt der hier entwickelten Theorie der kanonischen Ströme ein systematisches Verständnis der Zusammenhänge erlaubt.
Projektliteratur:
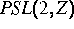, Bull. AMS 25 (1991), 55--60