|
|
|
[Contents] | [Index] |
Collaborator: B. Wagner
Cooperation with: A. Münch (Humboldt-Universität zu Berlin, Heisenberg Fellow at WIAS), T.P. Witelski (Duke University, Durham, USA), J. King (University of Nottingham, UK), R. Konrad, K. Jacobs (Universität des Saarlandes, Saarbrücken), M. Rauscher (Max-Planck-Institut für Metallforschung, Stuttgart), R. Blossey (Interdisciplinary Research Institute, IEMN, Lille, France)
Description:
The occurrence and the nature of slippage of liquids on solid surfaces is vividly discussed in the literature and is of large technological interest since a sliding fluid can flow faster through, e.g., microfluidic devices. In recent years, one major focus of interest has been the process of dewetting of polymer films (typically ranging on the scale of tens to a few hundred nanometers) from hydrophobic substrates. Understanding the dynamics and morphology of this process is particularly important for the design of microelectronic devices. Theoretical progress here depends strongly on the ability to develop, analyze, and solve reduced models, such as lubrication-type models for the film dynamics, thereby addressing the presence of highly separated scales (in space as well as in time) and the high (fourth) order of the involved partial differential equations.
Dewetting typically starts by the formation of holes due to spinodal decomposition or heterogeneous nucleation. As the holes grow, the displaced liquid collects in growing rims surrounding the holes. On longer time scales, the rims themselves are subject to a finger-type instability. In this project, we have derived lubrication models that account for large slip lengths. The slip length can be understood as the length below the solid/liquid interface where the velocity extrapolates to zero. We have developed numerical methods that explore the special structure of the models to yield, in combination with spatial adaptivity and parallelization, efficient codes for the dewetting process. Using linear stability analysis, we showed that, both under no-slip and full-slip boundary conditions, perturbations of the dewetting front are amplified, but the effect is greater by orders of magnitude in the full-slip case. Furthermore, the perturbations become much more asymmetrical under full-slip boundary conditions, while they develop symmetrical bulges under no-slip conditions, [3]. Additional computations that solve the lubrication model for the full three-dimensional flow confirm that these findings carry over to the nonlinear regime [2] and are in good agreement with the experimental findings, [8]. Our recent focus has been the development of multiple-scale asymptotic techniques in order to formulate simpler problems that are able to resolve the small-scale structure in the vicinity of the apparent contact line and asymptotically match the inner solution to those solving the large-scale outer problem describing the shape and dynamics of the rim. As a consequence, a further model reduction of the lubrication model to a corresponding sharp-interface model could be achieved. Here, the linear stability analysis is greatly simplified and could be investigated purely analytically, [6], [5], confirming our earlier numerical results on the linear stability of the evolving rims.
In this project, we derived lubrication models for dewetting thin
films from the Navier-Stokes equations for incompressible flow, which
are characterized by the orders of magnitude of the slip length. As
one traverses the ranges of the slip length, the flow field will
change from a parabolic flow field to what is essentially plug flow,
which implies a change from the balance of the pressure gradient with
the horizontal velocity to the balance of the pressure gradient with
the vertical velocity and thereby also a change of the velocity
scale. For small slip lengths (at most of the order of the height of
the film), we obtained the velocity scale
![]() =
= ![]()
![]() /
/![]() together with the
well-known dimension-reduced lubrication equation for the profile
h(x, t)
together with the
well-known dimension-reduced lubrication equation for the profile
h(x, t)
Re*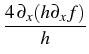 + h + h |
(2) |
As a first application we found that the strong slip regime could capture the rim profiles of dewetting nanoscale polymer films observed in experiments by R. Konrad and K. Jacobs.
In this project, we concentrated on the rim morphology affected by slippage. Our collaborators R. Konrad and K. Jacobs have performed experiments to compare the dewetting behavior of liquid polymer films on silicon/silicon oxide wafers that have been coated with either octadecyltrichlorosilane (OTS) or dodecyltrichlorosilane (DTS). The experiments show that the dewetting rates for DTS are significantly larger than for OTS. They also compared the profile of the rim that forms as the film dewets and found that it develops a spatially decaying oscillatory structure on the side facing the undisturbed film if an OTS-coated wafer is used, but is monotonically decaying for DTS. For this situation, only the solid/liquid friction coefficient can be different, suggesting that slippage plays a role in this transition. For the first time, we showed that this transition is in fact captured by a lubrication model that can be derived from the Navier-Stokes equations with a Navier-slip boundary condition at the liquid/solid interface, and accounts for large slip lengths; it is the strong slip model (2) introduced above.
For this model, an approximate description of the portion of the
profile of the dewetting rim that connects to the undistributed uniform
film h = 1 for
x![]()
![]() was developed to find the evolution of the film
near the flat state. The dominant contributions could be derived to obey the
ODE
-
was developed to find the evolution of the film
near the flat state. The dominant contributions could be derived to obey the
ODE
- ![]()
![]() Re
Re![]()
![]() = 4
= 4![]()
![]()
![]()
![]() +
+ ![]()
![]() -
- ![]()
![]() for the perturbation
for the perturbation ![]() about the flat state.
Here,
about the flat state.
Here,
![]() = x - s(t) and s(t) denotes the position of the contact line.
The normal mode solutions
= x - s(t) and s(t) denotes the position of the contact line.
The normal mode solutions
![]() (
(![]() ) = e
) = e![]()
![]() of this ODE, which
decay for
of this ODE, which
decay for
![]()
![]()
![]() , are spatially oscillating due to a pair
of complex conjugate
, are spatially oscillating due to a pair
of complex conjugate ![]() , if the discriminant
corresponding to the dispersion relation for
, if the discriminant
corresponding to the dispersion relation for ![]() ,
,
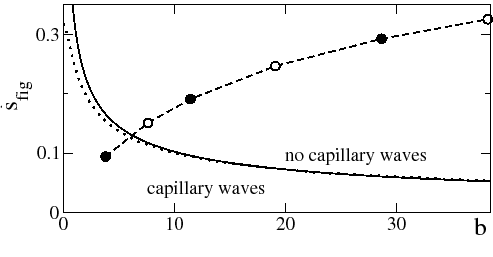 |
One observes that as b is increased, the dewetting rate increases, and for slip lengths larger than the threshold, the dashed line in Figure 1 leaves the region where capillary waves are expected. Inspection of the profile in a semilog plot of the profiles in Figure 2 showed a second maximum for the smallest b, indicating that we have the oscillatory structure of a wave.
These findings compared very well with the experimental results where on OTS-covered substrates, the rim of the dewetting PS film exhibits an oscillatory shape, whereas on DTS-covered surfaces, at the same temperature, no oscillation is observed, [7].
![\makeatletter
\@ZweiProjektbilderNocap[h]{0.45\textwidth}{prof-dim-final.eps}{profiles-final.eps}
\makeatother](img671.gif) |
In the range where the polymer chain length begins to be comparable with the film thickness, the dynamics of the thin films becomes non-Newtonian, leading to novel dynamical signatures. In order to describe such effects, various different models have been postulated in an ad hoc or, at best, a phenomenological manner, leading to controversies about the interpretation of experimental results.
Given the success of the lubrication approximation for the dynamics of
thin films of Newtonian character, we were prompted to look at this
issue for the case of non-Newtonian liquids and addressed the question
of the derivation of thin-film equations based on the lubrication
approximation for viscoelastic fluids, [10]. We introduced a
general model class of viscoelastic fluids which was the basis for our
derivation. Subsequently, we demonstrated how to derive thin-film
equations for the non-Newtonian liquid, stressing the underlying
physical assumptions. For the situations we have in mind, we assumed
the liquid to be incompressible with mass density ![]() . With this,
the equation of mass conservation reduces to
. With this,
the equation of mass conservation reduces to
![]() .
. ![]() = 0, with the velocity field
= 0, with the velocity field
![]() = (ux, uy, uz). The equation of momentum conservation is
= (ux, uy, uz). The equation of momentum conservation is
![]()
![]() = -
= - ![]() pR +
pR + ![]() .
. ![]() , with the reduced pressure pR = p + V. The hydrostatic pressure is
p, the pressure induced by external fields such as gravity or van
der Waals-type dispersion forces V, and the deviatoric (traceless)
part of the stress tensor is
, with the reduced pressure pR = p + V. The hydrostatic pressure is
p, the pressure induced by external fields such as gravity or van
der Waals-type dispersion forces V, and the deviatoric (traceless)
part of the stress tensor is
![]() (which is
symmetric). With
=
(which is
symmetric). With
= ![]()
![]() +
+ ![]() .
. ![]() , we
denote the materials (or total) derivative and with
, we
denote the materials (or total) derivative and with
![]() = (
= (![]() ,
,![]() ,
,![]() )
the gradient operator.
)
the gradient operator.
Starting with the co-rotational Jeffreys model, we found that in order to obtain a closed-form lubrication model, only the linear versions
with i = x, y, respectively, are in general allowed. For this we found for the lubrication approximation the following system![\begin{multline}
{\frac{\partial h}{\partial t}} +\lambda_2\left[\frac{\partial^...
...h}{\partial t}} {\boldsymbol{\nabla}}_{\!\!\vert\vert}p_R\right]
\end{multline}](img687.gif)
![\begin{multline}
u_i = -b h \partial_i p_R
+\left(\frac{z^2}{2}-h z\right) \...
...1-\frac{\lambda_1}{\lambda_2}\right) \partial_i p_R\right] dt'.
\end{multline}](img689.gif)
We presently discuss how the models we obtained relate to the phenomenological models discussed in the literature so far.
References:
|
|
|
[Contents] | [Index] |