Thermodynamic foundations for modeling saturated poroelastic

[Next]:

Projects interconnecting research groups

[Up]:

Projects

[Previous]:

Dynamics of thin dewetting liquid films

[Contents]

[Index]

Thermodynamic foundations for modeling saturated poroelastic bodies

Collaborator: K. Wilmanski

Description:

The modeling of thermoporoelastic materials which has been the subject of research for eight years has been completed in 2004. In particular, the following problems were solved

- The general form of the energy balance equation for thermoporoelastic materials: It has been shown, for instance, that the so-called simple mixture model yields in the Lagrangian description the following form of relation between the entropy flux $\bf H$ and the heat flux $\bf Q$ , [3], [4],

$\displaystyle \bf H$ = $\displaystyle {\frac{{1}}{{T}}}$ $\displaystyle \left(\vphantom{ {\bf Q-\rho }^{F}\psi ^{F}{\bf\acute{X}}% ^{F}}\right.$ $\displaystyle \bf Q-\rho^{{F}}_{}$ $\displaystyle \psi^{{F}}_{}$ $\displaystyle \bf\acute{X}^{{F}}_{}$ $\displaystyle \left.\vphantom{ {\bf Q-\rho }^{F}\psi ^{F}{\bf\acute{X}}% ^{F}}\right)$ , $\displaystyle \bf\acute{X}^{{F}}_{}$ = $\displaystyle \bf F^{{S-1}}_{}$ $\displaystyle \left(\vphantom{ {\bf\acute{x}}% ^{F}-{\bf\acute{x}}^{S}}\right.$ $\displaystyle \bf\acute{x}^{{F}}_{}$ - $\displaystyle \bf\acute{x}^{{S}}_{}$ $\displaystyle \left.\vphantom{ {\bf\acute{x}}% ^{F}-{\bf\acute{x}}^{S}}\right)$ ,

where T is the absolute temperature, $\psi^{{F}}_{}$ denotes the Helmholtz free energy of the fluid, $\bf F^{{S}}_{}$ is the deformation gradient of the skeleton, and $\bf\acute{x}^{{F}}_{}$ , $\bf\acute{x}^{{S}}_{}$ are velocities of components. This has also been proved in the case of a generalized model with a nonlinear dependence on the diffusion velocity $\bf\acute{X}^{{F}}_{}$ .

- It has been shown that the classical linear Biot model with added mass effects follows as a nonobjective approximation of a nonlinear model in which the following definition of the objective relative acceleration has been introduced, [4], [5],

$\displaystyle \bf a_{{r}}^{}$ = $\displaystyle {\frac{{\partial}}{{\partial t}}}$ $\displaystyle \left(\vphantom{ {\bf\acute{x}}^{F}-{\bf \acute{x}}^{S}}\right.$ $\displaystyle \bf\acute{x}^{{F}}_{}$ - $\displaystyle \bf\acute{x}^{{S}}_{}$ $\displaystyle \left.\vphantom{ {\bf\acute{x}}^{F}-{\bf \acute{x}}^{S}}\right)$ - $\displaystyle \left(\vphantom{ 1-{\frak{z}}}\right.$ 1 - $\displaystyle \frak{z}$ $\displaystyle \left.\vphantom{ 1-{\frak{z}}}\right)$ $\displaystyle \bf\acute{X}^{{F}}_{}$ ^.Grad $\displaystyle \bf\acute{x}^{{F}}_{}$ - $\displaystyle \frak{z}$ $\displaystyle \bf\acute{X}^{{F}}_{}$ ^. Grad $\displaystyle \bf\acute{x}^{{S}}_{}$ ,

where $\frak{z}$ is a material parameter. In the same work, it has been shown that the added mass effect cannot be related to tortuosity in spite of frequent claims in the literature.

- As the result of the micro-macro analysis [6], the balance equation for porosity has been corrected for an equilibrium contribution

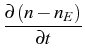$\displaystyle {\frac{{\partial \left( n-n_{E}\right) }}{{\partial t}}}$ + Div $\displaystyle \left(\vphantom{ \Phi _{0}{\bf\acute{X}}^{F}}\right.$ $\displaystyle \Phi_{{0}}^{}$ $\displaystyle \bf\acute{X}^{{F}}_{}$ $\displaystyle \left.\vphantom{ \Phi _{0}{\bf\acute{X}}^{F}}\right)$ = - $\displaystyle {\frac{{n-n_{E}}}{{\tau }}}$ ,

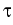
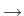
where n_E denotes the equilibrium porosity, and n_E, $\Phi_{{0}}^{}$ , $\tau$ are constitutive quantities, the latter being the relaxation time of porosity. In particular, in the linear Biot model ( $\tau$ $\rightarrow$ $\infty$ ), this equation yields the relation for porosity [6]

n = n_E + n₀ $\displaystyle {\frac{{\Phi }}{{n_{0}}}}$ $\displaystyle \left(\vphantom{ \varepsilon -\mbox{tr}{\bf e}% ^{S}}\right.$ $\displaystyle \varepsilon$ - tr $\displaystyle \bf e^{{S}}_{}$ $\displaystyle \left.\vphantom{ \varepsilon -\mbox{tr}{\bf e}% ^{S}}\right)$ , n_E = n₀ $\displaystyle \left(\vphantom{ 1+\delta \mbox{tr}{\bf e}^{S}}\right.$ 1 + $\displaystyle \delta$ tr $\displaystyle \bf e^{{S}}_{}$ $\displaystyle \left.\vphantom{ 1+\delta \mbox{tr}{\bf e}^{S}}\right)$ , $\displaystyle \varepsilon$ = $\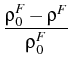displaystyle {\frac{{\rho _{0}^{F}-\rho ^{F}}}{{\rho _{0}^{F}}}}$ ,

where $\delta$ is the material constant. This relation checks with results of micro-macro transitions.

The model described above has been investigated in application to the description of linear and nonlinear waves. It has been shown ([4], [7], [1]) that linear acoustic waves correspond qualitatively with waves following from Biot's model. Quantitative discrepancies may be as large as 30 % and in some cases (e.g., attenuation), they indicate that the new model is physically better justified and in some cases (e.g., dependence of speeds on coupling of stresses), they are better within Biot's model. The new model yields also important results for surface waves (e.g., [2]). The analysis of nonlinear waves has been performed for the model in which material parameters are dependent on porosity, [8], [9]. It has been shown that for some physically justified cases, the P1 wave may yield the creation of strong discontinuities which have been attributed to the liquefaction. This conclusion is confirmed by comparison with theoretical results of Osinow within a one-component hypoplastic model and with experiments on Karlsruhe sands.

References:

B. ALBERS, K. WILMANSKI, On modeling acoustic waves in saturated poroelastic media, to appear in: J. Engrg. Mech.
, Monochromatic surface waves on impermeable boundaries in two-component poroelastic media, to appear in: Contin. Mech. Thermodyn.
K. WILMANSKI, Thermodynamics of simple two-component thermo-poroelastic media, in: Recent Trends and Applications of Mathematics to Mechanics, S. Rionero, G. Romano, eds., Springer, Milano, 2005.
, Tortuosity and objective relative accelerations in the theory of porous media, to appear in: Proc. Roy. Soc. London, Ser. A.
, Objective relative accelerations in theories of porous materials, in: Thermodynamische Materialtheorien, Workshop, December 12-18, 2004, vol. 55 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2004, pp. 36-37.
, On microstructural tests for poroelastic materials and corresponding Gassmann-type relations, Géotechnique, 54 (2004), pp. 593-603.
, Linear sound waves in poroelastic materials: Simple mixtures vs. Biot's model, to appear in: Trends in Applications of Mathematics to Mechanics, K. Hutter, Y. Wang, eds., Shaker-Verlag.
, Critical time for acoustic waves in weakly nonlinear poroelastic materials, to appear in: Contin. Mech. Thermodyn.
, Threshold to liquefaction in granular materials as a formation of strong wave discontinuities in poroelastic media, to appear in: Biot Centennial Conference, Oklahoma 2005, A. Cheng, ed.