Collaborator: A. Glitzky,
R. Hünlich
Cooperation with: L. Recke (Humboldt-Universität zu Berlin),
G. Wachutka (Technische Universität München)
Supported by: DFG:
``Energiemodelle für heterogene Halbleiterstrukturen'' (Energy models for heterogeneous semiconductor structures)
Description:
The charge transport in semiconductor devices is described by the
van Roosbroeck equations.
They consist of two continuity equations
for the densities n and p of
electrons e and holes h, respectively, and a
Poisson equation
for
the electrostatic potential 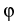 . Physical parameters occurring in these
equations depend on the device temperature T. Therefore, under nonisothermal
conditions a balance equation for the density of total energy must be
added, and a so-called energy model
arises
(see [1, 7]). Finally, if
incompletely ionized impurities
(for example, radiation-induced traps or other deep
recombination centers) are taken into account, we have to consider
further continuity equations for the densities of (in general immobile)
species
Xj,
j = 1,..., k. These species exist in different
charge states
which are transformed into each other by ionization reactions.
Let
Xj be an acceptor-like impurity
and let X- be its ion. Then we have to consider the reactions
. Physical parameters occurring in these
equations depend on the device temperature T. Therefore, under nonisothermal
conditions a balance equation for the density of total energy must be
added, and a so-called energy model
arises
(see [1, 7]). Finally, if
incompletely ionized impurities
(for example, radiation-induced traps or other deep
recombination centers) are taken into account, we have to consider
further continuity equations for the densities of (in general immobile)
species
Xj,
j = 1,..., k. These species exist in different
charge states
which are transformed into each other by ionization reactions.
Let
Xj be an acceptor-like impurity
and let X- be its ion. Then we have to consider the reactions
e- + Xj 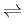 Xj-, h+ + Xj- Xj-, h+ + Xj- 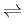 Xj. Xj.
|
(1) |
If
Xj is a donor-like impurity
and
Xj+ denotes its ion,
then the reactions are
e- + Xj+ 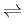 Xj, h+ + Xj Xj, h+ + Xj 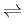 Xj+. Xj+.
|
(2) |
Moreover, a (direct) electron-hole recombination-generation
e- + h+ 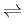 0 0
|
(3) |
takes place.
If
Xj is a donor (an acceptor), we denote by u2j-1
the density of
Xj (of
Xj-) and by u2j the density of
Xj+ (of
Xj).
Furthermore, we define charge numbers as follows:
q2j-1 : = 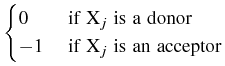 , q2j : = 1 + q2j-1, j = 1,..., k. , q2j : = 1 + q2j-1, j = 1,..., k. |
|
|
|
Then the stationary energy model for devices with incompletely ionized
impurities has the form
-  . ( . (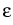  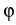 ) = f0 - n + p + ) = f0 - n + p + 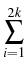 qiui, qiui, . je = 0, . je = 0,
|
(4) |
 . jn = R0 + . jn = R0 + 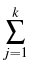 Rj1, Rj1, . jp = R0 + . jp = R0 + 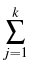 Rj2, Rj2,
|
(5) |
|
Rj1 = Rj2, u2j-1 + u2j = fj, j = 1,..., k.
|
(6) |
Here jn, jp denote the particle flux densities of electrons and holes,
Rj1, Rj2, and R0 denote the reaction rates of the first and
second reaction in (1) or in (2), respectively,
and of the reaction (3). Moreover,
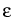 is the dielectric permittivity and f0, fj are a
charge density and particle densities which must be prescribed.
The system has to be completed by suitable
state equations for the species
e, h,
X1,..., X2k and kinetic relations.
is the dielectric permittivity and f0, fj are a
charge density and particle densities which must be prescribed.
The system has to be completed by suitable
state equations for the species
e, h,
X1,..., X2k and kinetic relations.
Special isothermal models of this kind are presented in [6].
There also results of
simulations with WIAS-TeSCA
are compared with
experimental results.
First, under reliable assumptions
concerning the state equations and kinetic relations
we eliminate the constraints from the system
by evaluating the subsystem (6).
We end up with a system of four
strongly coupled equations with nonlinear source terms depending on
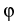 , T, on the electrochemical potentials
, T, on the electrochemical potentials
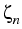 ,
, 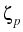 of
electrons and holes, on f0, and on the local invariants
fj, j = 1,..., k.
The resulting stationary energy model
can be written in the form
of
electrons and holes, on f0, and on the local invariants
fj, j = 1,..., k.
The resulting stationary energy model
can be written in the form
where
with conductivities 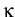 > 0,
> 0,
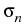 ,
, 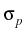 > 0,
> 0,
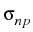
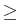 0,
and transported entropies Pn, Pp depending in a nonsmooth way on x and
smoothly on the state variables.
Let
0,
and transported entropies Pn, Pp depending in a nonsmooth way on x and
smoothly on the state variables.
Let 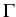 be the boundary of the domain
be the boundary of the domain  , which is occupied
by the heterogeneous semiconductor device.
, which is occupied
by the heterogeneous semiconductor device. 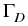 and
and 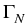 denote disjoint, relatively open parts of
denote disjoint, relatively open parts of 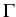 with
mes(
with
mes(
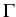
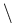 (
(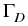
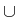
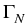 )) = 0. For (7) we
suppose mixed boundary conditions
of the form
)) = 0. For (7) we
suppose mixed boundary conditions
of the form
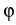 = vD1, = vD1, | T = vD2, | 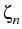 = vD3, = vD3, | 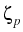 = vD4 = vD4 | on 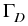 , , |
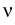 . ( . (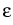  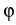 ) = g1, ) = g1, | - 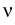 . je = g2, . je = g2, | - 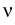 . jn = g3, . jn = g3, | - 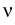 . jp = g4 . jp = g4 | on 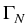 . . |
|
(8) |
We use the vectors
v = (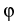 , T,
, T,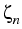 ,
,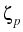 ),
vD = (vD1,..., vD4),
g = (g1,..., g4),
f = (f0, f1,..., fk), and the triplet
of data
w = (vD, g, f )
and look for weak solutions of (7),(8)
in the form
v = V + vD, where vD is a function
fulfilling the Dirichlet boundary conditions vD and V represents the
homogeneous part of the solution.
),
vD = (vD1,..., vD4),
g = (g1,..., g4),
f = (f0, f1,..., fk), and the triplet
of data
w = (vD, g, f )
and look for weak solutions of (7),(8)
in the form
v = V + vD, where vD is a function
fulfilling the Dirichlet boundary conditions vD and V represents the
homogeneous part of the solution.
We assume that
the boundary values vDi, i = 1, 2, 3, 4, are traces of
W1, p functions viD, p > 2
and find
W1, q formulations
(q  (2, p]) for that system of equations,
(2, p]) for that system of equations,
F(
V,
w) = 0,
V 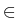 W1, q0
W1, q0(
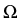
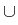
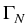
)
4,
w 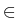 W1-1/p, p
W1-1/p, p(
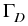
)
4 x L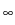
(
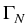
)
4 x L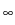
(
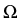
)
x {
h 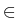 L
L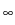
(
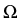
) : essinf
h > 0}
k.
Using techniques from [5], the operator F turns out to be
continuously differentiable.
If
w* = (vD*, g*, f*) is fixed such that
vDi* = const, i = 2, 3, 4,
vD3* + vD4* = 0,
vD2* > 0,
and
g* = (g1*, 0, 0, 0),
then there exists a solution V* of
F(V*, w*) = 0 which represents a thermodynamic equilibrium.
We prove that for suitable q > 2
the linearization
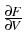 (V*, w*)
is a linear isomorphism from
W1, q0(
(V*, w*)
is a linear isomorphism from
W1, q0(
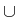
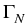 )4
onto
W1, q'(
)4
onto
W1, q'(
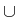
 )*4.
Here we use regularity results for strongly coupled elliptic systems
with mixed boundary conditions stated in [4].
We apply the Implicit Function Theorem
to obtain that
for
w = (vD, g, f ) near w*, the equation
F(V, w) = 0 has a unique solution V near
V*.
Details and the precise assumptions of our investigations may be found in
[3].
)*4.
Here we use regularity results for strongly coupled elliptic systems
with mixed boundary conditions stated in [4].
We apply the Implicit Function Theorem
to obtain that
for
w = (vD, g, f ) near w*, the equation
F(V, w) = 0 has a unique solution V near
V*.
Details and the precise assumptions of our investigations may be found in
[3].
In [2],
we investigated a more general energy model with m different species where
all species were assumed to be mobile such that the stationary energy model
corresponds to an elliptic system with
m + 2 equations.
References:
- G. ALBINUS, H. GAJEWSKI, R. HÜNLICH,
Thermodynamic design of energy models of
semiconductor devices,
Nonlinearity, 15 (2002),
pp. 367-383.
- A. GLITZKY, R. HÜNLICH,
Stationary solutions of two-dimensional heterogeneous
energy models with multiple species,
Banach Center Publ., 66 (2004), pp. 135-151.
,
Stationary energy models for semiconductor devices with incompletely
ionized impurities,
WIAS Preprint no. 1001, 2005,
submitted.
- K. GRÖGER,
A W1, p-estimate for solutions to mixed boundary value problems
for second order elliptic differential equations,
Math. Ann., 283 (1989), pp. 679-687.
- L. RECKE,
Applications of the implicit function theorem to
quasi-linear elliptic boundary value problems with non-smooth data,
Comm. Partial Differential Equations, 20 (1995), pp. 1457-1479.
- R. SIEMIENIEC, W. SÜDKAMP, J. LUTZ,
Determination of parameters of
radiation induced traps in silicon,
Solid-State Electronics, 46 (2002),
pp. 891-901.
- G. WACHUTKA,
Rigorous thermodynamic treatment of heat generation and conduction
in semiconductor device modelling,
IEEE Trans. CAD, 9 (1990), pp. 1141-1149.
LaTeX typesetting by H. Pletat
2005-07-29
![]() . Physical parameters occurring in these
equations depend on the device temperature T. Therefore, under nonisothermal
conditions a balance equation for the density of total energy must be
added, and a so-called energy model
arises
(see [1, 7]). Finally, if
incompletely ionized impurities
(for example, radiation-induced traps or other deep
recombination centers) are taken into account, we have to consider
further continuity equations for the densities of (in general immobile)
species
Xj,
j = 1,..., k. These species exist in different
charge states
which are transformed into each other by ionization reactions.
Let
Xj be an acceptor-like impurity
and let X- be its ion. Then we have to consider the reactions
. Physical parameters occurring in these
equations depend on the device temperature T. Therefore, under nonisothermal
conditions a balance equation for the density of total energy must be
added, and a so-called energy model
arises
(see [1, 7]). Finally, if
incompletely ionized impurities
(for example, radiation-induced traps or other deep
recombination centers) are taken into account, we have to consider
further continuity equations for the densities of (in general immobile)
species
Xj,
j = 1,..., k. These species exist in different
charge states
which are transformed into each other by ionization reactions.
Let
Xj be an acceptor-like impurity
and let X- be its ion. Then we have to consider the reactions
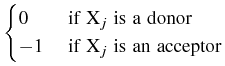 , q2j : = 1 + q2j-1, j = 1,..., k.
, q2j : = 1 + q2j-1, j = 1,..., k.![]() , T, on the electrochemical potentials
, T, on the electrochemical potentials
![]() ,
, ![]() of
electrons and holes, on f0, and on the local invariants
fj, j = 1,..., k.
The resulting stationary energy model
can be written in the form
of
electrons and holes, on f0, and on the local invariants
fj, j = 1,..., k.
The resulting stationary energy model
can be written in the form
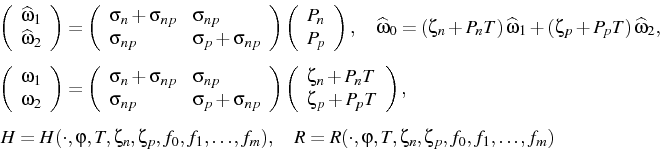
![]() (2, p]) for that system of equations,
(2, p]) for that system of equations,