Phenomenological modeling of drift-diffusion processes

[Next]:

Research Group Laser Dynamics

[Up]:

Projects

[Previous]:

Stationary energy models for semiconductor devices

[Contents]

[Index]

Phenomenological modeling of drift-diffusion processes

Collaborator: H. Stephan

Cooperation with: G. Wachutka (Technische Universität München), E.Ya. Khruslov (B. Verkin Institute for Low Temperature Physics and Engineering, Kharkov, Ukraine)

Supported by: DFG: ``Energiemodelle für heterogene Halbleiterstrukturen'' (Energy models for heterogeneous semiconductor structures)

Description:

Drift-diffusion equations provide a powerful description of microscopic particle transport on the phenomenological level. However, the relation between the phenomenological description and the underlying microscopic transport phenomena, in general, is not clear-cut. Often only special solutions (the stationary solution), global properties (the free energy) or functionals of the solution (moments) are known. Therefore it is interesting to consider example problems which are non-trivial and the underlying microscopic processes are well known. We demonstrate this in two examples.

Ex. 1: A powerful thermodynamically consistent method for deriving drift-diffusion equations has been developed in the last years by H. Gajewski and others (see [1, 2, 3]). Looking for a phenomenological evolution equation for a concentration u(x, t) with u(x, t) $\geq$ 0, $\int_{\Omega}^{}$ u(x, t) $\equiv$ 1 ( x $\in$ $\Omega$ $\subset$ $\mathbb {R}$ _n, t $\geq$ 0), we consider at first a microscopic picture. Let u(x, t) be the solution of a Kolmogorov-Chapman equation

$\displaystyle {\partial \over \partial t}$ u

$\displaystyle \bf A$ u,

(1)

where the linear operator $\bf A$ is of the form (+ suitable boundary conditions)

( $\displaystyle \bf A$ f )(x) = $\displaystyle \sum\limits_{{i,j=1}}^{n}$ $\displaystyle {\partial^2 \over \partial x_i\partial x_j}$ $\displaystyle \Big($ b_ij(x)f (x) $\displaystyle \Big)$ - $\displaystyle \sum\limits_{{i=1}}^{n}$ $\displaystyle {\partial \over \partial x_i}$ $\displaystyle \Big($ a_i(x)f (x) $\displaystyle \Big)$ + $\displaystyle \mean\int_\Omega \Big(\! Q(x',x) f(x') - Q(x,x') f(x)\!\! \Big)dx'.$

(2)

Here, a_i(x), b_ij(x), and Q(x, x') $\geq$ 0 are suitable coefficient functions, and $\bf B$ = (b_ij(x)) is a non-negative matrix. The integral is to be understood as a principle value integral. Let u^*(x) be a stationary solution of Au^* = 0. Equations (1)-(2) are the general form of a linear evolution equation conserving positivity u(x, t) $\geq$ 0 and norm $\int_{\Omega}^{}$ u(x, t)dx = 1. Moreover, it can be shown, see [4], that every more or less arbitrary convex function F : $\mathbb {R}$ $\longrightarrow$ $\mathbb {R}$ , normalized by F(1) = 0, generates a time-decreasing Lyapunov function,

H(t) = $\displaystyle \Phi$ (u) = $\displaystyle \int_{\Omega}^{}$ F $\displaystyle \left(\vphantom{ {u(x,t) \over u^*(x)} }\right.$ $\displaystyle {u(x,t) \over u^*(x)}$ $\displaystyle \left.\vphantom{ {u(x,t) \over u^*(x)} }\right)$ u^*(x)dx , H(t₁) $\displaystyle \geq$ H(t₂) $\displaystyle \geq$ 0, t₂ $\displaystyle \geq$ t₁ .

(3)

Now we are going to derive a phenomenological equation for u by Gajewski's method, assuming that a free energy of type (3), with some reference concentration u^*, is given. This is a typical situation in applications.

We calculate the stationary state u_s(x) by Lagrange's method, varying the functional $\Phi$ (u) under the constraint $\int_{\Omega}^{}$ u(x, t)dx = 1. This leads to the functional L(u) = $\Phi$ (u) - $\lambda$ $\left(\vphantom{ \int_\Omega u(x) dx - 1}\right.$ $\int_{\Omega}^{}$ u(x)dx - 1 $\left.\vphantom{ \int_\Omega u(x) dx - 1}\right)$ . Thus, u_s(x) is the solution to the Euler-Lagrange equation

$\displaystyle \lambda$ = $\displaystyle \varphi$ $\displaystyle \left(\vphantom{ {u_s(x) \over u^*(x)}}\right.$ $\displaystyle {u_s(x) \over u^*(x)}$ $\displaystyle \left.\vphantom{ {u_s(x) \over u^*(x)}}\right)$ $\displaystyle \Longleftrightarrow$ u_s(x) = $\displaystyle \varphi^{{-1}}_{}$ ( $\displaystyle \lambda$ )u^*(x)

with the monotone function $\varphi$ (z) = F'(z). From $\int_{\Omega}^{}$ u^*(x)dx = $\int_{\Omega}^{}$ u_s(x)dx = 1 we get $\lambda$ = $\varphi$ (1). It follows u_s = u^*, as expected.

For deriving an evolution equation, we assume that the Lagrange multiplier $\lambda$ is the chemical potential depending on x and t, and

u(x, t) = $\displaystyle \varphi^{{-1}}_{}$ ( $\displaystyle \lambda$ (x, t))u^*(x)

is the state equation. Let $\bf D$ be a linear operator with $\bf D$ 1 = 0. We assume that bfD $\lambda$ is the driving force of the diffusion vanishing in the stationary state $\lambda$ = const., and postulate an equation for u of the form

$\displaystyle {\partial \over \partial t}$ u(x, t) = - $\displaystyle \bf D^{*}_{}$ $\displaystyle \bf\sigma$ $\displaystyle \bf D$ $\displaystyle \lambda$

(4)

with some suitable operator $\boldsymbol\sigma$ . Equations of this type satisfy some desired basic properties: All solutions are normalized

$\displaystyle {d \over dt}$ $\displaystyle \langle$ 1, u(t) $\displaystyle \rangle$ = $\displaystyle \langle$ 1, $\displaystyle \dot{{u}}$ (t) $\displaystyle \rangle$ = - $\displaystyle \langle$ 1, $\displaystyle \bf D^{*}_{}$ $\displaystyle \mbox{$\boldsymbol{\sigma}$}$ $\displaystyle \bf D$ $\displaystyle \lambda$ $\displaystyle \rangle$ = - $\displaystyle \langle$ $\displaystyle \bf D$ 1, $\displaystyle \mbox{$\boldsymbol{\sigma}$}$ $\displaystyle \bf D$ $\displaystyle \lambda$ $\displaystyle \rangle$ = 0

( $\langle$ ^.,^. $\rangle$ is the dual pairing) and the free energy is monotone

$\displaystyle {d \over dt}$ $\displaystyle \Phi$ $\displaystyle \big($ u(t) $\displaystyle \big)$ = $\displaystyle \left<\vphantom{ \varphi\left( {u(t) \over u^*} \right),\dot{u}(t) }\right.$ $\displaystyle \varphi$ $\displaystyle \left(\vphantom{ {u(t) \over u^*} }\right.$ $\displaystyle {u(t) \over u^*}$ $\displaystyle \left.\vphantom{ {u(t) \over u^*} }\right)$ , $\displaystyle \dot{{u}}$ (t) $\displaystyle \left.\vphantom{ \varphi\left( {u(t) \over u^*} \right),\dot{u}(t) }\right>$ = - $\displaystyle \left<\vphantom{ \lambda , {\bf D}^* \mbox{$\boldsymbol{\sigma}$} {\bf D} \lambda}\right.$ $\displaystyle \lambda$ , $\displaystyle \bf D^{*}_{}$ $\displaystyle \mbox{$\boldsymbol{\sigma}$}$ $\displaystyle \bf D$ $\displaystyle \lambda$ $\displaystyle \left.\vphantom{ \lambda , {\bf D}^* \mbox{$\boldsymbol{\sigma}$} {\bf D} \lambda}\right>$ = - $\displaystyle \left<\vphantom{ \mbox{$\boldsymbol{\sigma}$} {\bf D} \lambda,{\bf D} \lambda}\right.$ $\displaystyle \mbox{$\boldsymbol{\sigma}$}$ $\displaystyle \bf D$ $\displaystyle \lambda$ , $\displaystyle \bf D$ $\displaystyle \lambda$ $\displaystyle \left.\vphantom{ \mbox{$\boldsymbol{\sigma}$} {\bf D} \lambda,{\bf D} \lambda}\right>$ $\displaystyle \leq$ 0 ,

if $\boldsymbol\sigma$ is positive definite. Moreover, to prove the positivity of the solution of such equations can be a hard problem. Since $\boldsymbol\sigma$ can depend on u or the gradient of u, equation (4) can be nonlinear.

We have to choose $\bf D$ and $\boldsymbol\sigma$ in such a manner that the equations (4) and (1) describe the same physical problem. As usual, $\bf D$ is taken as a gradient $\bf D$ = $\bf G$ $\nabla$ with an n x n matrix $\bf G$ (x). There is good reason, see [3] and the references there, to take $\boldsymbol\sigma$ similar to the inverse Hessian of $\Phi$

$\displaystyle \mbox{$\boldsymbol{\sigma}$}$ = $\displaystyle \mu$ u^* $\displaystyle \varphi{^\prime}$ $\displaystyle \left(\vphantom{ {u \over u^*}}\right.$ $\displaystyle {u \over u^*}$ $\displaystyle \left.\vphantom{ {u \over u^*}}\right)^{{-1}}_{}$

with some positive function $\mu$ (x). Then (4) becomes

$\displaystyle {\partial \over \partial t}$ u(x, t) = $\displaystyle \nabla$ $\displaystyle \bf G^{*}_{}$ $\displaystyle \mu$ $\displaystyle \bf G$ $\displaystyle \left(\vphantom{ \nabla u - u \nabla \log u^* }\right.$ $\displaystyle \nabla$ u - u $\displaystyle \nabla$ log u^* $\displaystyle \left.\vphantom{ \nabla u - u \nabla \log u^* }\right)$ ,

(5)

a typical drift-diffusion equation widely used in semiconductor analysis, chemotaxis, and phase separation, [1, 2, 3]. On the other hand, this is the Fokker-Planck equation, a special case of (1)-(2) with Q = 0, $\bf B$ = $\bf G^{*}_{}$ $\mu$ $\bf G$ , and a_i(x) = $\sum_{j}^{}$ ${\partial \over \partial x_j}$ b_ij(x) + ${1 \over u^*(x)}$ ${\partial \over \partial x_j}$ u^*(x), and therefore it conserves positivity. This and the linearity of equation (5) favor the inverse Hessian among other choices for $\boldsymbol\sigma$ .

Ex. 2: An other typical situation is the following: We want to derive an equation for u(x, t) of type (4) for the diffusion of particles in a space-homogeneous medium. However, for an exact description of the problem we have to take into account more state parameters than x, e.g., the velocity v, too. Let v $\in$ $\mathbb {R}$ and x $\in$ $\mathbb {R}$ . Let us assume that the trajectory in phase space is Markovian with the probability density W(v, x, t). Then the Kolmogorov-Chapman equation describing the time evolution of W(v, x, t) has the form

$\displaystyle {\partial \over \partial t}$ W(v, x, t) = AW - v $\displaystyle {\partial \over \partial x}$ W, W(v, x, 0) = w₀(v)u₀(x) ,

(6)

where A is a linear operator of type (2) acting only on the parameter v.

Ultimately, we are only interested in the concentration (space density) u(x, t) = $\int_{{\mathbb{R}}}^{}$ W(v, x, t)dv. A typical method to calculate u is to derive a system of equations for the v-moments of W and close this system in a heuristic way. In the case of the general Brownian motion, governed by equation (6) and

( $\displaystyle \bf A$ f )(v) = $\displaystyle {\partial\over {\partial v}}$ $\displaystyle \big($ avf $\displaystyle \big)$ + b $\displaystyle {{\partial^2} \over {\partial v^2}}$ f + $\displaystyle \mean\int\nolimits_{{\mathbb{R}}} {\big( Q(v-v') f (v') - Q(v'-v)f (v) \big) dv'} ,$

with constants a and b > 0, this can be done rigorously without further heuristic arguments (see [5]). For simplicity, let us assume that the velocity is already relaxed. This means the initial value w₀ is the stationary velocity density, i.e., $\bf A$ w₀ = 0. It turns out that u(x, t) is the solution of the non-autonomous equation

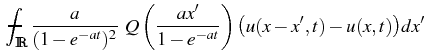$\displaystyle {\partial \over \partial t}$ u(x, t) = $\displaystyle {b \over a^2}$ $\displaystyle \big($ 1 - e^-at $\displaystyle \big)$ $\displaystyle {{\partial^2} \over {\partial x^2}}$ u(x, t) + $\displaystyle \mean\int\nolimits_{{\mathbb{R}}} {a\over (1 - e^{-a t})^2} Q\left({ax'\over 1 - e^{-a t}}\right) \big( u(x-x',t)-u(x,t) \big) dx'$

with initial data c(x, 0) = c₀(x), whereas the original physical problem is autonomous.

In the limit t $\longrightarrow$ $\infty$ we get the equation

$\displaystyle {\partial \over {\partial t}}$ u(x, t)

$\displaystyle {b \over a^2}$ $\displaystyle {{\partial^2} \over {\partial x^2}}$ u(x, t) + $\displaystyle \mean\int\nolimits_{{\mathbb{R}}} aQ(ax') \big( u(x-x',t)-u(x,t) \big) dx' .$

For Q = 0 this is the diffusion equation which is parabolic.

In the limit t $\longrightarrow$ 0 we get the second-order hyperbolic equation

$\displaystyle {\partial^2 \over \partial t^2}$ u(x, t) = $\displaystyle {b + q \over 2a}$ $\displaystyle {{\partial^2} \over {\partial x^2}}$ u(x, t) ,

where Q(v) = Q(- v) and q = $\int$ v²Q(v)dv.

References:

G. ALBINUS, H. GAJEWSKI, R. HÜNLICH, Thermodynamic design of energy models of semiconductor devices, Nonlinearity, 16 (2002), pp. 367-383.
H. GAJEWSKI, K. ZACHARIAS, Global behaviour of a reaction-diffusion system modelling chemotaxis, Math. Nachr., 195 (1998), pp. 77-114.
J.A. GRIEPENTROG, On the unique solvability of a phase separation problem for multicomponent systems, Banach Center Publ., 66 (2004), pp. 153-164.
H. STEPHAN, Lyapunov functions for positive linear evolution problems, WIAS Preprint no. 978, 2004, submitted.
, A dimension-reduced description of general Brownian motion by non-autonomous diffusion-like equations, WIAS Preprint no. 994, 2004, submitted.