[Next]:

Optimization of the sparse direct solver

[Up]:

Projects

[Previous]:

Projects

 [Contents] 

 [Index] 

Algorithms for the solution of the semiconductor device equations in three dimensions with application to DEPFET sensor design

Collaborator: K. Gärtner

Cooperation with: R. Richter (Halbleiterlabor (Semiconductor Laboratory), Max-Planck-Institut für Physik, München, und Max-Planck-Institut für extra-terrestrische Physik, Garching)

Description: The main goal is the development of improved algorithms for the numerical solution of degenerate systems of elliptic and parabolic partial differential equations based on discretizations, fulfilling qualitative stability properties, known from the analytic equations, too.

The semiconductor device equations can be seen as an example out of a much larger class of problems, but they are well understood in many respects, sufficiently hard to solve and of practical interest--hence a good candidate to deal with. The interest starts with grid generation, includes properties of the equations and their discretization, effective algorithms for the solution, and ends with solving some selected real-world problems.

The present status of the work is roughly characterized by:

• A basic level of the models (for recombination, transport phenomena, etc.);
• A general geometry and boundary descriptions using tetrahedral Delaunay grids;
• Three different Newton methods based on different decoupling techniques together with the use of iterative and direct simulation methods (PARDISO,  see page ) to solve the stationary equations and to compare their efficiency and robustness;
• The use (expansion) of 2D numerically given doping profiles is possible now.

The present results are:

• A 3D prototype code (SMP parallel in the essential parts, using a completely weak formulation of the finite volume discretization) for discussing and investigating some issues of interest in the more general pdelib2 (see page ) design, including basic algorithms;
• The transfer of specific algorithms to WIAS-TeSCA;
• And some contribution by ``insight'' into computed potential and density distributions to the design of a DEPFET sensor at the Semiconductor Laboratory in Munich.

To illustrate the status from the application point of view, a summary of the device function is given: the DEPFET combines detection and amplification within one device, [1]. A p-channel MOSFET or JFET (junction field effect transistor, contacts SOURCE, GATE, DRAIN) is integrated onto a silicon detector substrate, which becomes fully depleted by the application of a sufficiently high negative voltage to a backside p+ contact (BACK). By means of sideward depletion, a potential minimum is formed which is shifted directly underneath the transistor channel at a depth of about 1 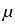$\mu$m below the GATE contact. Incident photons and particles generate electron-hole pairs within the fully depleted bulk. While the holes drift into the back contact, electrons are accumulated in the potential minimum, called the internal gate. The resulting change of the JFET current is a measure of the collected amount of charge and the deposited energy, respectively.

The readout of the device is non-destructive and can be repeated several times. For removing signal electrons and thermally generated charges from the internal gate, a clear structure is integrated into the device (contacts CLEAR and CLEAR-GATE). The efficiency of the clear process determines the readout noise essentially. Understanding this process is the point where 3D device simulations enter. Due to the very low input capacitance the inherent noise during amplification becomes very low. Equivalent noise charges of about two electrons were measured at room temperature on recently fabricated structures.

DEPFET detectors can be applied for XRAY spectroscopy, e.g., in space or biomedical experiments ([2], [3]) as well as for particle detection, for instance, in vertex detectors ([4]).

The pictures (generated by gltools) show the electron and hole density (log₁₀) in a section of a sensor element. The grid is highly anisotropic and has a resolution of order 10 nm close to the contacts. The computational domain of 18x28x50 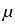$\mu$m³ size is discretized by 156000 nodes. The numerical challenges are introduced by the floating regions and the very small recombination, resulting in density variations of 25 orders of magnitude.

The I-V curves show some properties of the detector for different boundary and doping conditions. The device performance depends strongly on doping concentration, geometric parameters, and boundary conditions.

Numerical challenges for the future are, for instance, faster algorithms to allow higher resolution and time-dependent computations on better grids (TetGen, see page ). Investigations of the interaction of two or more pixel sensor elements may be another task introducing a new level of complexity.

References:

1. J. KEMMER, G. LUTZ, New semiconductor detector concepts, Nucl. Instr. & Meth., A253 (1987), pp. 365-377.

2. G. LUTZ, R.H. RICHTER, L. STRÜDER, New novel pixel detectors for X-ray astronomy and other applications, Nucl. Instr. & Meth., A461 (2001), pp. 393-404.

3. W. NEESER ET AL., The DEPFET pixel BIOSCOPE, IEEE Trans. Nucl. Sci., 47 (2000), pp. 1246-1250.

4. R.H. RICHTER ET AL., Design and technology of DEPFET pixel sensors for linear collider applications, Nucl. Instr. & Meth., A511 (2003), pp. 250-256.

Fig. 1: I-V curves (top), log₁₀ of the electron (middle) and hole densities (bottom) at the top and a vertical cut (cut at y = 14 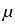 $\mu$m, grey relief) of the detector.
(The contact areas on top of the device can be identified by the following codes (e, h: color), where e denotes the electron density and h the holes density pictures above: CLEAR (e: red), CLEAR-GATE (e, h: light blue), DRAIN (in the cut of region), GATE (h: orange), SOURCE (h: red), floating region (h: yellow).)

[Next]:

Optimization of the sparse direct solver

[Up]:

Projects

[Previous]:

Projects

 [Contents] 

 [Index]