<tt>pdelib</tt> - Algorithms and software components

[Next]:

Research Group Nonlinear Optimization and Inverse

[Up]:

Projects

[Previous]:

Numerical simulation of Direct Methanol Fuel

[Contents]

[Index]

Subsections

`pdelib` - Algorithms and software components for the numerical solution of partial differential equations

Collaborator: J. Fuhrmann, K. Gärtner, H. Langmach, M. Uhle, H. Si

Cooperation with: A. Linke (Freie Universität Berlin (FU-FZT 86))

Supported by: DFG-Forschungszentrum ``Mathematik für Schlüsseltechnologien'' (Research Center ``Mathematics for Key Technologies'' (FZT 86)), project C1

Description: The purpose of this project is the further development of pdelib, a toolbox of software components for the numerical solution of partial differential equations. Current project works focus on the re-design of the whole code.

**Fig. 1:** Preliminary results for parallel speedup for Laplace operator
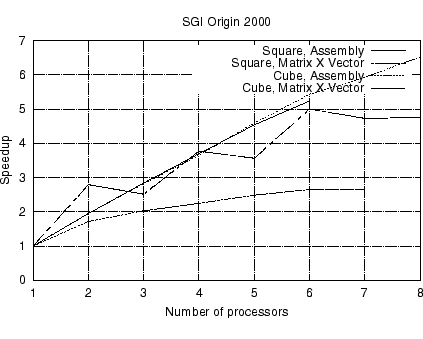$\ProjektEPSbildNocap{0.5\textwidth}{speedup.eps}$

The main features being implemented are

Solver kernel which runs efficiently on single processor workstations and multiprocessor SMP architectures using OpenMP or pthreads. The API is targeted at ease of use of the parallel features while not giving up code efficiency;
Support for a wide class of problems including finite volumes for systems of convection/diffusion/reaction equations, Navier-Stokes equations, and higher order finite elements;
Integration of the Delaunay mesh generators triangle [1] (2D) and TetGen (3D). This allows to describe geometries in the extension language Lua or in the C code and thus offers a large amount of flexibility for grid adaptation and geometry modification;
Parameter input and solver control can use the Lua [3] extension language;
Online visualization of the solution process based on OpenGL.

**Fig. 2:** Mesh subdivided for running calculations on four processors with separators removed
$\ProjektEPSbildNocap{0.5\textwidth}{747.eps}$

The main aim of the efforts during the reporting period was to bring the pdelib2 code into a state where it can be used in application projects. We focused on the following issues:

Grid partitioning

We assume that grid generators produce grids which are described by an array of node coordinates, an array of cells characterized by the adjacent node numbers, an array of cell region numbers, an array of boundary faces characterized by the adjacent node numbers, and an array of boundary region numbers.

Grid partitioning in pdelib2 has the following aims:

Given a number of processors nproc, subdivide the sets of cells, resp. boundary faces resp. nodes into partitions. To each of the partitions we assign a color in such a way that neighboring partitions appear in different colors. If possible, nproc partitions shall correspond to each of the colors.
This is motivated by the assumption that all partitions with one color can be processed in parallel without write conflicts by nproc processors during assembly and preconditioning.
Given a number ncache of cells, re-arrange cells and boundary faces into homogeneous zones stored consecutively. Homogeneity means that each zone belongs to exactly one region and exactly one partition.
Behind this lies the assumption that all data for assembly on ncache elements fit into the cache and can be processed utilizing superscalar features of modern processor architectures.

Partitioning is performed recursively in several steps with the help of the METIS [4] package.

A loop over the grid after partitioning then has the following hierarchical structure:

        loop over all partition colors
                  #pragma omp parallel 
                           loop over all partitions with given color 
                           loop over all zones of the partition
                                   loop over all elements  of a zone

The user needs to write code for the inner two loops while the outer loop and the parallel loop are hidden, opening the possibility for varying the implementation.

**Fig. 3:** Regions, partitions, and zones for a DMFC contact plate
$\makeatletter \@DreiProjektbilderNocap[h]{0.3\textwidth}{regions.eps}{partitions.eps}{zones.eps} \makeatother$

J.R. SHEWCHUK, Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator, in: Applied Computational Geometry: Towards Geometric Engineering, M.C. Lin, D. Manocha, eds. Springer, Berlin, 1996, pp. 203-222.
B. SPITZAK ET AL., FLTK - the Fast Light Toolkit.
URL: http://www.fltk.org.
R. IERUSALIMSCHY, L.H. DE FIGUEIREDO, W. CELES, Lua - an extensible extension language, Software: Practice & Experience, 26 (1996), pp. 635-652.
URL: http://www.lua.org.
G. KARYPIS, V. KUMAR, Metis - family of multilevel partitioning algorithms.
URL: http://www-users.cs.umn.edu/ karypis/metis/
D. VAN HEESCH, Doxygen documentation tool.
URL: http://www.doxygen.org.
J. FUHRMANN, Multiphysics systems solution by time-implicit Voronoi box finite volumes, in: Proceedings of the Third Symposium on Finite Volumes in Complex Applications, Porquerolles, France, June 2002, F. Benkhaldoun, R. Vilsmeier, eds., Hermes, Paris, 2002, pp. 551-559.